题目内容
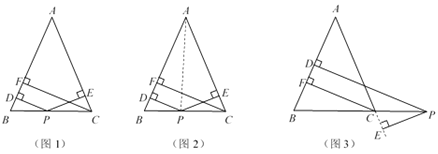
【题目】已知长方形ABCD中,AD=10cm,AB=6cm,点M在边CD上,由C往D运动,速度为1cm/s,运动时间为t秒,将△ADM沿着AM翻折至△ADM,点D对应点为D,AD所在直线与边BC交于点P.
(1)如图1,当t=0时,求证:PA=PC;
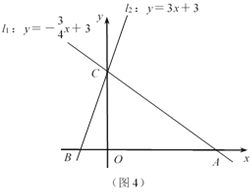
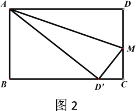
(2)如图2,当t为何值时,点D恰好落在边BC上;
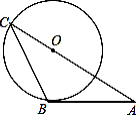
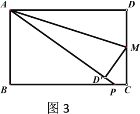
(3)如图3,当t=3时,求CP的长.
 (
(
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】
(1)由折叠性质可得![]() ADC
ADC![]() A DC可得∠DAC=∠DAC, 在长方形ABCD中,AD//BC,可得 ∠DAC=∠BCA,从而得到∠DAC=∠BCA,即可得出结论。
A DC可得∠DAC=∠DAC, 在长方形ABCD中,AD//BC,可得 ∠DAC=∠BCA,从而得到∠DAC=∠BCA,即可得出结论。
(2)由折叠性质可得![]() ADC
ADC![]() A DC可得DM=DM=6-t,AD=A D=10,根据勾股定理可得B D=8则C D=2,在Rt
A DC可得DM=DM=6-t,AD=A D=10,根据勾股定理可得B D=8则C D=2,在Rt![]() CM D中,根据勾股定理列出方程即可。
CM D中,根据勾股定理列出方程即可。
(3)当t=3时,CM=DM=3, 连接PM,根据HL证得![]() M DP
M DP![]() MCP,可得DP=PC, ∠DMP=∠CMP, 由折叠性质可得得出∠AMD=∠AMD,从而证得∠AMP=90
MCP,可得DP=PC, ∠DMP=∠CMP, 由折叠性质可得得出∠AMD=∠AMD,从而证得∠AMP=90![]() ,再根据
,再根据![]() ADM
ADM![]() MDP即可。
MDP即可。
(1)当t=0时,M与C重合
由折叠性质可得![]() ADC
ADC![]() A DC
A DC
∴∠DAC=∠DAC,
在长方形ABCD中,AD//BC,
∴ ∠DAC=∠BCA
∴∠DAC=∠BCA,
∴PA=PC;
(2)由折叠性质可得![]() ADC
ADC![]() A DC
A DC
∴DM=DM=6-t,AD=A D=10,
在Rt![]() ABD中,B D=
ABD中,B D=![]() =8
=8
∴DC=BC- B D=10-8=2cm
在Rt![]() CMD中,
CMD中,
∴![]()
解得:t=![]()
∴当t=![]() 时,点D恰好落在边BC上;
时,点D恰好落在边BC上;
(3)当t=3时,CM=DM= DM=3,
由折叠性质可得:∠ADM=∠D=90![]()

连接PM,
在Rt![]() M DP和Rt
M DP和Rt![]() MCP中
MCP中
![]()
∴![]() M DP
M DP![]() MCP,
MCP,
∴DP=PC, ∠DMP=∠CMP,
∵∠AMD=∠AMD
∴∠PMD+∠AMD=90![]()
∵∠MAP +∠AMD=90![]()
∴∠PMD=∠MAP
∵∠ADM=∠PDM
∴![]() M DA
M DA![]() P DM
P DM
∴![]()
∴![]() = P D. A D
= P D. A D
∴![]() = P D.10
= P D.10
∴P D=![]()
∴CP=![]()