Question

【题目】对于数轴上的三点，给出如下定义：若其中一个点与其他两个点的距离恰好满足2倍的数量关系，则称该点是其他两点的“倍联点”. 例如数轴上点所表示的数分别为1，3，4，满足，此时点是点的“倍联点”.

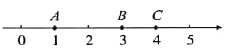
若数轴上点表示，点表示6，回答下列问题：

（1）数轴上点分別对应0，3. 5和11，则点_________是点的“倍联点”，点是________这两点的“倍联点”；

（2）已知动点在点的右侧，若点是点的倍联点，求此时点表示的数.

Answer 1

【答案】（1）；，（2）点表示的数为24或.

【解析】

（1）分别计算D1，D2，D3三点与M,N的距离，再根据新定义的概念得到答案；
（2）设点表示的数为，分以下情况列方程求解：①；②.

解：（1）D1M=3，D1N=6，2D1M=D1N，故D1符合题意；
D2M=6.5，D2N=2.5，故D2不符合题意；
D3M=14，D3N=5，故D3不符合题意；

因此点D1是点的“倍联点”．
又2D2N= D3N，∴点N是D2，D3的“倍联点”.

故答案为：D1;D2，D3.

（2）设点表示的数为，

第一种情况：当时，

则，

解得.

第二种情况：当时，

则，

解得：.

综上所述，点表示的数为24或.