题目内容
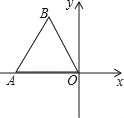
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.
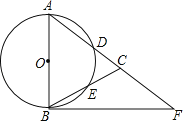
(1)试判断直线BF与⊙O的位置关系,并说明理由;
(2)若AB=6,BF=8,求tan∠CBF.
【答案】(1)BF为⊙O的切线;理由详见解析;(2)![]() .
.
【解析】
试题分析:(1)连接AE.通过AB⊥BF,点B在⊙O上可以推知BF为⊙O的切线;
(2)作辅助线CG(过点C作CG⊥BF于点G)构建平行线AB∥CG.由“平行线截线段成比例”知![]() =
=![]() =
=![]() ,从而求得FG的值;然后根据图形中相关线段间的和差关系求得直角三角形CBG的两直角边BG、CG的长度;最后由锐角三角函数的定义来求tan∠CBF的值.
,从而求得FG的值;然后根据图形中相关线段间的和差关系求得直角三角形CBG的两直角边BG、CG的长度;最后由锐角三角函数的定义来求tan∠CBF的值.
试题解析:(1)BF为⊙O的切线.理由如下:
连接AE.
∵AB为⊙O的直径,
∴∠AEB=90°(直径所对的圆周角是直角),
∴∠BAE+∠ABE=90°(直角三角形的两个锐角互余);
又∵AB=AC,AE⊥BC,
∴AE平分∠BAC,即∠BAE=∠CAE;
∵∠CAB=2∠CBF,
∴∠BAE=∠CBF,
∴∠BAE+∠ABE=∠ABE+∠CBF=90°,即AB⊥BF,
∵OB是半径,
∴BF为⊙O的切线;
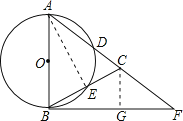
(2)过点C作CG⊥BF于点G.
在Rt△ABF中,AB=6,BF=8,
∴AF=10(勾股定理);
又∵AC=AB=6
∴CF=4;
∵CG⊥BF,AB⊥BF,
∴CG∥AB,
∴![]() =
=![]() =
=![]() ,(平行线截线段成比例),
,(平行线截线段成比例),
∴FG=![]() ,
,
由勾股定理得:CG=![]() =
=![]() ,
,
∴BG=BF﹣FG=8﹣![]() =
=![]() ,
,
在Rt△BCG中,tan∠CBF=![]() =
=![]() .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)在第__________次记录时距![]() 地最远;
地最远;
(2)求收工时距![]() 地多远?
地多远?
(3)若每千米耗油![]() 升,每升汽油需
升,每升汽油需![]() 元,问检修小组工作一天需汽油费多少元?
元,问检修小组工作一天需汽油费多少元?