题目内容
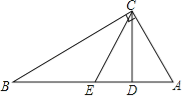
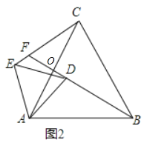
【题目】如图,△ABC是边长为6的等边三角形,点D、E分别是边AB、AC的中点,将△ADE绕点A旋转,BD与CE所在的直线交于点F.
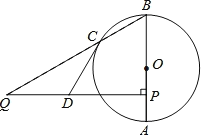
(1)如图(2)所示,将△ADE绕点A逆时针旋转,且旋转角不大于60°,∠CFB的度数是多少?说明你的理由?
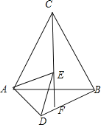
(2)当△ADE绕点A旋转时,若△BCF为直角三角形,求出线段BF的长.

【答案】(1)∠CFB=60°,理由见解析;(2)4![]() 或2
或2![]() .
.
【解析】
(1)根据等边三角形的性质得到AC=AB,∠EAD=∠CAB=60°,由点D、E分别是边AB、AC的中点,得到AE=AD,根据旋转的性质得到∠EAC=∠BAD,根据全等三角形的性质得到∠ACE=∠ABD,由对顶角相等得∠COF=∠AOB,根据三角形的内角和即可得到结论;
(2)根据含30°角的直角三角形的性质,利用勾股定理解直角三角形,分两种情况求解即可得到结论.
解:(1)∠CFB=60°,
理由:∵△ABC是等边三角形,
∴AC=AB,∠CAB=60°,
∵点D、E分别是边AB、AC的中点,
∴![]()
∴AE=AD,
∵将△ADE绕点A旋转,BD与CE所在的直线交于点F,
∴∠EAC=∠BAD,
在△ACE与△ABD中,
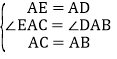 ,
,
∴△ACE≌△ABD,
∴∠ACE=∠ABD,设AC交BF于O,
∵∠COF=∠AOB,
∴∠CFB=∠CAB=60°;
(2)∠CFB=60°,∠BCF=90°时,∠CBF=30°,
∴CF =![]() BF,
BF,![]()
∴![]() ,
,
解得:BF=4![]() ;
;
∠CFB=60°,∠CBF=90°时,∠BCF=30°,
∴CF =2BF,![]()
∴![]()
解得:BF = 2![]() .
.
故答案为:(1)∠CFB=60°,理由见解析;(2)4![]() 或2
或2![]() .
.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目