题目内容
【题目】在△ABC中,AB=AC,D、E分别在BC、AC上,AD=AE,∠CDE=20°,则∠BAD的度数为（ ）
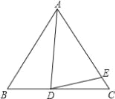
A. 36° B. 40° C. 45° D. 50°
【答案】B
【解析】
利用三角形的外角可得到：∠ADE+∠EDC =∠BAD+∠B，∠ADE=∠AED=∠C+∠EDC，然后进行代换得到∠C+∠BAD=∠C+20°+20°，即可求得答案．
∵∠ADC是三角形ABD的外角，∠AED是三角形DEC的一个外角，∠CDE=20°，∴∠ADC=∠BAD+∠B=∠ADE+∠EDC，∠AED=∠EDC+∠C，∠B+∠BAD=∠ADE+20°，∠AED=∠C+20°．
∵AB=AC，AD=AE，∠CDE=20°，∴∠B=∠C，∠ADE=∠AED=∠C+20°，∴∠C+∠BAD=∠C+20°+20°，∴∠BAD=40°．
故选B．
练习册系列答案
相关题目
