题目内容
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,CD=h,AB=c,下面有3个命题:(1)
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,CD=h,AB=c,下面有3个命题:(1) ;(2)a+b<c+h;(3)以a+b,h,c+h为边的三角形是直角三角形.其中正确命题的个数是
;(2)a+b<c+h;(3)以a+b,h,c+h为边的三角形是直角三角形.其中正确命题的个数是
- A.0
- B.1
- C.2
- D.3
D
分析:(1)先根据勾股定理用a、b表示出AB的长,再由S△ABC= AC•BC=
AC•BC= AB•CD解答即可;
AB•CD解答即可;
(2)先证(3)a+b,h,c+h为边的三角形是直角三角形成立,再由三角形的三边关系求解;
(3)先分别求出(a+b)2,h2,(c+h)2的值,再根据勾股定理的逆定理进行判断即可.
解答:(1)∵Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=b,BC=a,CD=h,AB=c,
∴c= ,
,
∴S△ABC= ab=
ab= ch,
ch,
∴h= ,h2=
,h2=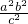 ,
,
∴ =
=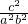 ,即
,即 =
= =
= ,故(1)正确;
,故(1)正确;
(2)∵ ab=
ab= ch,
ch,
∴ab=ch,即a2b2=c2h2,
∴(a+b)2-a2-b2=(c+h)2-c2-h2,
∴(c+h)2-(a+b)2=c2-a2-b2+h2,
∵a2+b2=c2,
∴(c+h)2-(a+b)2=h2,
∵h>0,且a b c h均为线段.
∴a>0,b>0,c>0,h>0,
∴c+h>a+b,故(3)正确;
(3)∵(c+h)2=c2+2ch+h2;
h2+(a+b)2=h2+a2+2ab+b2,a2+b2=c2(勾股定理),ab=ch(面积公式推导),
∴c2+2ch+h2=h2+a2+2ab+b2,
∴(c+h)2=h2+(a+b)2,
∴根据勾股定理的逆定理知道以h,c+h,a+b为边构成的三角形是直角三角形,故正确.
故选D.
点评:本题考查的是勾股定理的逆定理及三角形的面积公式,熟知勾股定理的逆定理是解答此题的关键.
分析:(1)先根据勾股定理用a、b表示出AB的长,再由S△ABC=
 AC•BC=
AC•BC= AB•CD解答即可;
AB•CD解答即可;(2)先证(3)a+b,h,c+h为边的三角形是直角三角形成立,再由三角形的三边关系求解;
(3)先分别求出(a+b)2,h2,(c+h)2的值,再根据勾股定理的逆定理进行判断即可.
解答:(1)∵Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=b,BC=a,CD=h,AB=c,
∴c=
 ,
,∴S△ABC=
 ab=
ab= ch,
ch,∴h=
 ,h2=
,h2=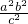 ,
,∴
 =
=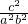 ,即
,即 =
= =
= ,故(1)正确;
,故(1)正确;(2)∵
 ab=
ab= ch,
ch,∴ab=ch,即a2b2=c2h2,
∴(a+b)2-a2-b2=(c+h)2-c2-h2,
∴(c+h)2-(a+b)2=c2-a2-b2+h2,
∵a2+b2=c2,
∴(c+h)2-(a+b)2=h2,
∵h>0,且a b c h均为线段.
∴a>0,b>0,c>0,h>0,
∴c+h>a+b,故(3)正确;
(3)∵(c+h)2=c2+2ch+h2;
h2+(a+b)2=h2+a2+2ab+b2,a2+b2=c2(勾股定理),ab=ch(面积公式推导),
∴c2+2ch+h2=h2+a2+2ab+b2,
∴(c+h)2=h2+(a+b)2,
∴根据勾股定理的逆定理知道以h,c+h,a+b为边构成的三角形是直角三角形,故正确.
故选D.
点评:本题考查的是勾股定理的逆定理及三角形的面积公式,熟知勾股定理的逆定理是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离. 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直. 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).