题目内容
如图,已知四边形ABCD是梯形,AD∥BC,∠B=∠C,试说明AB=CD.

答案:
解析:
解析:
|
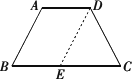
分析:在梯形中添加辅助线的方法很多,具体解答时,必须根据题目中的条件和图形,灵活运用三角形和平行四边形的有关知识. 方法一:平移梯形的一腰,将梯形转化为平行四边形和三角形来解决. 解:如图,过点D作DE∥AB,交BC于点E.
因为AD∥BC, 所以四边形ABED是平行四边形. 所以AB=DE,∠B=∠DEC. 又因为∠B=∠C,所以∠DEC=∠C. 所以CD=DE,即AB=CD. 方法二:延长梯形的两腰相交于一点,将梯形转化为三角形来解决. 解:如图,延长BA、CD相交于点E.
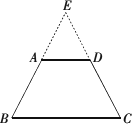
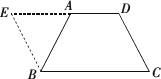
因为AD∥BC, 所以∠EAD=∠B,∠EDA=∠C. 又因为∠B=∠C, 所以∠EAD=∠EDA. 所以EB=EC,EA=ED. 所以EB-EA=EC-ED. 所以AB=CD. 方法三:过梯形下底的一个顶点作一腰的平行线与上底的延长线相交于一点,将梯形转化为平行四边形来解决. 解:如图,可过点B作BE∥CD,交DA的延长线于点E.
因为 AD∥BC,所以四边形EBCD是平行四边形. 所以BE=CD,∠E=∠C,∠EAB=∠ABC. 又因为∠ABC=∠C,所以∠E=∠EAB. 所以AB=BE=CD. |

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且 (2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
(2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
