题目内容
【题目】定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
(1)判断:一个内角为120°的菱形 等距四边形.(填“是”或“不是”)
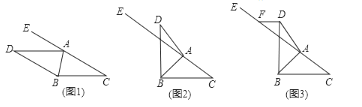
(2)如图2,在5×5的网格图中有A、B两点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.端点均为非等距点的对角线长为 端点均为非等距点的对角线长为
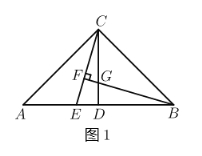
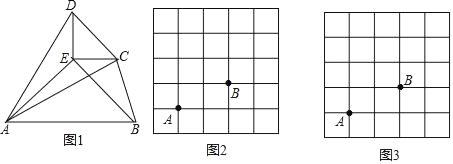
(3)如图1,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连结AD,AC,BC,若四边形ABCD是以A为等距点的等距四边形,求∠BCD的度数.
【答案】(1)是;(2)见解析;(3)150°.
【解析】
(1)由菱形的性质和等边三角形的判定与性质即可得出结论;
(2)根据题意画出图形,由勾股定理即可得出答案;
(3)由SAS证明△AEC≌△BED,得出AC=BD,由等距四边形的定义得出AD=AB=AC,证出AD=AB=BD,△ABD是等边三角形,得出∠DAB=60°,由SSS证明△AED≌△AEC,得出∠CAE=∠DAE=15°,求出∠DAC=∠CAE+∠DAE=30°,∠BAC=∠BAE﹣∠CAE=30°,由等腰三角形的性质和三角形内角和定理求出∠ACB和∠ACD的度数,即可得出答案.
解:(1)一个内角为120°的菱形是等距四边形;
故答案为:是;
(2)如图2,图3所示:
在图2中,由勾股定理得: ![]()
在图3中,由勾股定理得: ![]()
故答案为:![]()
(3)解:连接BD.如图1所示:
∵△ABE与△CDE都是等腰直角三角形,
∴DE=EC,AE=EB,
∠DEC+∠BEC=∠AEB+∠BEC,
即∠AEC=∠DEB,
在△AEC和△BED中,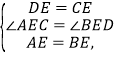 ,
,
∴△AEC≌△BED(SAS),
∴AC=BD,
∵四边形ABCD是以A为等距点的等距四边形,
∴AD=AB=AC,
∴AD=AB=BD,
∴△ABD是等边三角形,
∴∠DAB=60°,
∴∠DAE=∠DAB﹣∠EAB=60°﹣45°=15°,
在△AED和△AEC中,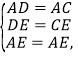
∴△AED≌△AEC(SSS),
∴∠CAE=∠DAE=15°,
∴∠DAC=∠CAE+∠DAE=30°,∠BAC=∠BAE﹣∠CAE=30°,
∵AB=AC,AC=AD,
∴![]()
∴∠BCD=∠ACB+∠ACD=75°+75°=150°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案