题目内容
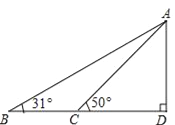
【题目】如图,半圆O的直径DE=10cm,△ABC中,∠ACB=90°,∠ABC=30°,BC=10cm,半圆O以1cm/s的速度从右到左运动,在运动过程中,D、E点始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的右侧,OC=6cm,那么,当t为_____s时,△ABC的一边所在直线与半圆O所在的圆相切.

【答案】1或6或11或26
【解析】如图所示,
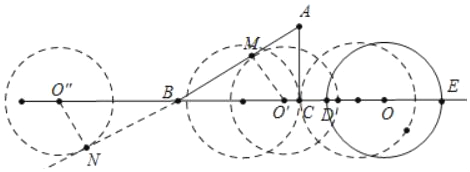
∵OC=6,DE=10,
∴OD=OE=5,CD=1,EC=11,
∴t=1或11s时,⊙O与直线AC相切;
当⊙O′与AB相切时,设切点为M,连接O′M,
在Rt△BMO′中,BO′=2MO′=10,
∴OO′=6,
当⊙O″与AB相切时,设切点为N,连接O′N,同法可得BO″=10,OO″=26,
∴当t=6或26s时,⊙O与AB相切.
故答案为1或6或11或26

练习册系列答案
相关题目
【题目】儿童服装店老板以50元的价格购进20件衣服,针对不同的顾客,20件衣服的售价不完全相同,若以68元为标准,将超出的钱数记为正,不足的钱数记为负,记录结果如下表:
售出件数 | 5 | 4 | 2 | 1 | 7 | 1 |
售价 | +2 | +3 | +1 | 0 | —2 | —1 |
(1)问该服装店售完这20件衣服后,赚了多少钱?
(2)老板为了促销,对购买价格不低于标准的每个顾客送了价值5元的小礼物,如果不考虑其他因素,这20件衣服实际赚了多少?