题目内容
【题目】已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.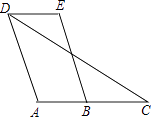
求证:∠A=∠E.
证明:∵∠EDC=∠C,
∴AB∥ . ()
∴ = . ()
∵AD∥BE,
∴∠A= . ()
∴∠A=∠E.(等量代换)
【答案】DE;内错角相等,两直线平行;∠E;∠EBC;两直线平行,内错角相等;∠EBC;两直线平行,同位角相等
【解析】证明:∵∠EDC=∠C,
∴AB∥DE(内错角相等,两直线平行),
∴∠E=∠EBC(两直线平行,内错角相等),
∵AD∥BE,
∴∠A=∠EBC(两直线平行,同位角相等),
∴∠A=∠E.(等量代换),
所以答案是:DE,内错角相等,两直线平行,∠E,∠EBC,两直线平行,内错角相等,∠EBC,两直线平行,同位角相等.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目