题目内容
【题目】已知,D、E分别为等边三角形ABC边上的点,AD=CE,BD、AE交于N,BM⊥AE于M.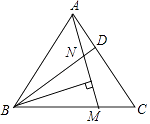
证明:
(1)∠CAE=∠ABD;
(2)MN= ![]() BN.
BN.
【答案】
(1)
证明:如图所示:
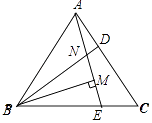
∵△ABC为等边三角形,
∴AC=AB,∠BAC=∠C=60°,
在△ABD和△CAE中, 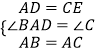 ,
,
∴△ABD≌△CAE(SAS),
∴∠CAE=∠ABD
(2)
证明:由(1)得∠CAE=∠ABD, ∵∠CAE+∠BAE=60°,
∴∠BAE+∠ABD=60°
∴∠BNM=∠BAN+∠ABN=60°,
∵BM⊥AE,
∴∠BMN=90°,
∴∠MBN=30°,
∴MN= ![]() BN.
BN.
【解析】(1)与等边三角形的性质得出AC=AB,∠BAC=∠C=60°,由SAS证明△ABD≌△CAE,得出∠CAE=∠ABD即可;
(2)由(1)得∠CAE=∠ABD,求出∠BNM=∠BAN+∠ABN=60°,得出∠BMN=90°,∠MBN=30°,由含30°角的直角三角形的性质即可得出结论.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.

练习册系列答案
相关题目