题目内容
【题目】如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF.
(1)求证:OE=OF;
(2)那么当点O运动到AC的中点时,试判断四边形AECF的形状并说明理由;
(3)在(2)的前提下△ABC满足什么条件,四边形AECF是正方形?说明理由.

【答案】(1)证明见解析;(2)四边形AECF是矩形;(3)四边形AECF是正方形.
【解析】
(1)由平行线的性质和角平分线的性质,推出∠ECB=∠CEO,∠GCF=∠CFO,∠ECB=∠ECO,∠GCF=∠OCF,通过等量代换即可推出∠CEO=∠ECO,∠CFO=∠OCF,便可确定OC=OE,OC=OF,可得OE=OF;
(2)当O点运动到AC的中点时,四边形AECF为矩形,根据矩形的判定定理(对角线相等且互相平分的四边形为矩形),结合(1)所推出的结论,即可推出OA=OC=OE=OF,求出AC=EF后,即可确定四边形AECF为矩形;
(3)当△ABC是直角三角形时,四边形AECF是正方形,根据(2)所推出的结论,由AC⊥BC,MN∥BC,确定AC⊥EF,即可推出结论.
证明:(1)
如图:
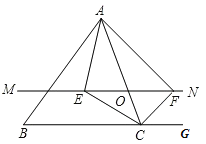
∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠GCF,
∵CE平分∠BCO,CF平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EO=FO.
(2)当点O运动到AC的中点时,四边形AECF是矩形.
∵当点O运动到AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵由(2)知,当点O运动到AC的中点时,四边形AECF是矩形,
∵MN∥BC,当∠ACB=90°,
∴∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案