Question

过半径为r的圆O的直径AB上一点P，作PC⊥AB交圆周于C．若要以PA、PB、PC为边作三角形，求OP长的范围．

Answer 1

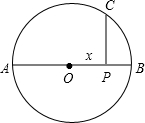解：不失一般性，令P在OB上，
且x=OP＞0，
则有AP＞BP，AP＞PC．
若以AP、BP、PC为边作三角形，
结合上面条件，
只须BP+PC＞AP，即PC＞r+x-r+x=2x，
又PC＞0，x≥0，
∴PC²＞4x²，（1）
又PC²=AP•BP=（r+x）（r-x）=r²-x²．
代入（1）得r²-x²＞4x²，
解得：．
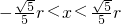∴OP的取值范围是．
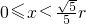分析：不失一般性，令P在OB上，且x=OP＞0，若以AP、BP、PC为边作三角形，只须BP+PC＞AP，即PC＞r+x-r+x=2x，再根据PC²＞4X²，解得OP长的范围．
点评：本题主要考查垂径定理和三角形三边的关系的知识点，解答本题的关键是数形结合，此题有一定的难度．