题目内容
(2011•攀枝花)如图(Ⅰ),在平面直角坐标系中,⊙O′是以点O′(2,﹣2)为圆心,半径为2的圆,⊙O″是以点O″(0,4)为圆心,半径为2的圆.
(1)将⊙O′竖直向上平移2个单位,得到⊙O1,将⊙O″水平向左平移1个单位,得到⊙O2如图(Ⅱ),分别求出⊙O1和⊙O2的圆心坐标.
(2)两圆平移后,⊙O2与y轴交于A、B两点,过A、B两点分别作⊙O2的切线,交x轴与C、D两点,求△O2AC和△O2BD的面积
.
解:(1)∵﹣2+2=0,
∴点O1的坐标为:(2,0),
∵0﹣1=﹣1,
∴点O2的坐标为:(﹣1,4);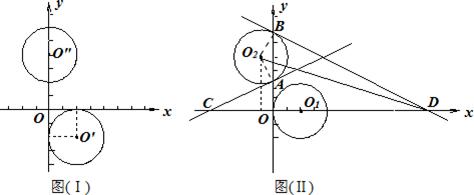
(2)如图,连接O2A,O2B,∵⊙O2的半径为2,圆心O2到y轴的距离是1,
∴∠O2AB=∠O2BA=30°,
∴AB=2×2cos30°=2 ,
,
∴点A、B的坐标分别为A(0,4﹣ ),B(0,4+
),B(0,4+ ),
),
∵AC,BD都是⊙O2的切线,
∴∠OAC=180°﹣90°﹣30°=60°,
∠OBD=90°﹣30°=60°,
∴AC=(4﹣ )÷cos60°=8﹣2
)÷cos60°=8﹣2 ,
,
BD=(4+ )÷cos60°=8+2
)÷cos60°=8+2 ,
,
∴S△O2AC= ×AC×O2A=
×AC×O2A= ×(8﹣2
×(8﹣2 )×2=8﹣2
)×2=8﹣2 ,
,
S△O2BD= ×BD×O2B=
×BD×O2B= ×(8+2
×(8+2 )×2=8+2
)×2=8+2 .
.
故答案为:8﹣2 ,8+2
,8+2 .
.
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(2011•攀枝花)下列各命题中,真命题是( )
| A.对角线相等且互相垂直的四边形是正方形 | |
| B.如果两个三角形有两条边和一个角分别对应相等,那么这两个三角形一定全等 | |
| C.角平分线上任意一点到这个角的两边的距离相等 | D.相等的圆周角所对的弧相等 |
(2011•攀枝花)要使 有意义,则x应该满足( )
有意义,则x应该满足( )
 有意义,则x应该满足( )
有意义,则x应该满足( )| A.0≤x≤3 | B.0<x≤3且x≠1 |
| C.1<x≤3 | D.0≤x≤3且x≠1 |
 +(1﹣π)0+
+(1﹣π)0+ .
.
 树状图或列表法加以说明.
树状图或列表法加以说明.