题目内容
如图(Ⅰ),在平面直角坐标系中,⊙O′是以点O′(2,-2)为圆心,半径为2的圆,⊙O″是以点O″(0,4)为圆心,半径为2的圆.(1)将⊙O′竖直向上平移2个单位,得到⊙O1,将⊙O″水平向左平移1个单位,得到⊙O2如图(Ⅱ),分别求出⊙O1和⊙O2的圆心坐标.
(2)两圆平移后,⊙O2与y轴交于A、B两点,过A、B两点分别作⊙O2的切线,交x轴与C、D两点,求△O2AC和△O2BD的面积.
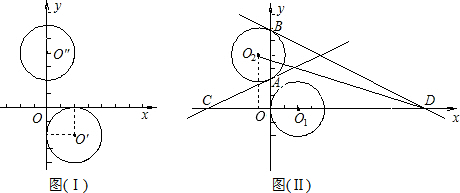
分析:(1)根据“左减右加,下减上加”的规律对点O′,O″的坐标进行平移即可得到点O1,O2的坐标;
(2)先求出点A、B的坐标,然后连接O2A,O2B,根据直角三角形30度角所对的直角边等于斜边的一半得出∠O2AB=∠O2BA=30°,又AC与BD是圆的切线,然后求出∠OAC=∠OBD=60°,利用特殊角的三角函数与点A,B的坐标即可求出AC、BD的长,最后代入三角形的面积公式进行计算即可.
(2)先求出点A、B的坐标,然后连接O2A,O2B,根据直角三角形30度角所对的直角边等于斜边的一半得出∠O2AB=∠O2BA=30°,又AC与BD是圆的切线,然后求出∠OAC=∠OBD=60°,利用特殊角的三角函数与点A,B的坐标即可求出AC、BD的长,最后代入三角形的面积公式进行计算即可.
解答:解:(1)∵-2+2=0,
∴点O1的坐标为:(2,0),
∵0-1=-1,
∴点O2的坐标为:(-1,4);
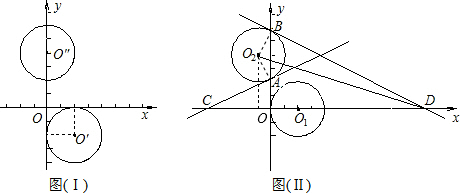
(2)如图,连接O2A,O2B,∵⊙O2的半径为2,圆心O2到y轴的距离是1,
∴∠O2AB=∠O2BA=30°,
∴AB=2×2cos30°=2
,
∴点A、B的坐标分别为A(0,4-
),B(0,4+
),
∵AC,BD都是⊙O2的切线,
∴∠OAC=180°-90°-30°=60°,
∠OBD=90°-30°=60°,
∴AC=(4-
)÷cos60°=8-2
,
BD=(4+
)÷cos60°=8+2
,
∴S△O2AC=
×AC×O2A=
×(8-2
)×2=8-2
,
S△O2BD=
×BD×O2B=
×(8+2
)×2=8+2
.
故答案为:8-2
,8+2
.
∴点O1的坐标为:(2,0),
∵0-1=-1,
∴点O2的坐标为:(-1,4);

(2)如图,连接O2A,O2B,∵⊙O2的半径为2,圆心O2到y轴的距离是1,
∴∠O2AB=∠O2BA=30°,
∴AB=2×2cos30°=2
| 3 |
∴点A、B的坐标分别为A(0,4-
| 3 |
| 3 |
∵AC,BD都是⊙O2的切线,
∴∠OAC=180°-90°-30°=60°,
∠OBD=90°-30°=60°,
∴AC=(4-
| 3 |
| 3 |
BD=(4+
| 3 |
| 3 |
∴S△O2AC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
S△O2BD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:8-2
| 3 |
| 3 |
点评:本题主要考查了切线的性质与坐标的平移,利用数据的特点求出30度角是解题的关键,也是解答本题的难点与突破口,本题难度适中,有一定的综合性.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
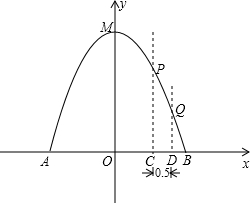 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系. 水柱在与池中心的水平距离为1m处达到最高,高度为3m.
水柱在与池中心的水平距离为1m处达到最高,高度为3m.




