题目内容
对于0<b<a,有关系a2-6b2=-ab,则化简
÷
等于( )
| a3-b3 |
| 3ab2 |
| a2+ab-2b2 |
| 2b2+3ab+a2 |
| A、3.5 | ||
| B、a+b | ||
C、
| ||
D、
|
分析:由式子a2-6b2=-ab,可以变形为a2-6b2+ab=0,即(a+2b)(a-3b)=0,即可得到a=2b,代入代数式即可求解.
解答:解:∵a2-6b2=-ab,可以变形为a2-6b2+ab=0,
即(a-2b)(a+3b)=0,
又∵0<b<a,则a+3b>0,
∴a-2b=0,
∴a=2b,
把a=2b代入
÷
,
=
•
,
=
•
,
=
,
=3.5.
故选A.
即(a-2b)(a+3b)=0,
又∵0<b<a,则a+3b>0,
∴a-2b=0,
∴a=2b,
把a=2b代入
| a3-b3 |
| 3ab2 |
| a2+ab-2b2 |
| 2b2+3ab+a2 |
=
| 8b3-b3 |
| 6b3 |
| 2b2+6b2+4b2 |
| 4b2+2b2-2b2 |
=
| 7b3 |
| 6b3 |
| 12b2 |
| 4b2 |
=
| 7 |
| 2 |
=3.5.
故选A.
点评:本题主要考查了分式的变形,把变形后的式子a=2b代入,正确进行化简是解题关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知一次函数y1=2x,二次函数y2=x2+1.
(Ⅰ)根据表中给出的x的值,计算对应的函数值y1、y2,并填在表格中:
(Ⅱ)观察第(Ⅰ)问表中有关的数据,证明如下结论:在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1≤y2均成立;
(Ⅲ)试问,是否存在二次函数y3=ax2+bx+c,其图象经过点(-5,2),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值y1≤y3≤y2均成立?若存在,求出函数y3的解析式;若不存在,请说明理由.
(Ⅰ)根据表中给出的x的值,计算对应的函数值y1、y2,并填在表格中:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y1=2x | |||||||
| y2=x2+1 |
(Ⅲ)试问,是否存在二次函数y3=ax2+bx+c,其图象经过点(-5,2),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值y1≤y3≤y2均成立?若存在,求出函数y3的解析式;若不存在,请说明理由.
 20、同学:你去过黄山吗?在黄山的上山路上,有一些断断续续的台阶,如图是其中的甲、乙段台阶路的示意图,图8中的数字表示每一级台阶的高度(单位:cm).并且数d、e、e、c、c、d的方差p,数据b、d、g、f、a、h的方差q,(10cm<a<b<c<d<e<f<g<h<20cm,且 p<q),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
20、同学:你去过黄山吗?在黄山的上山路上,有一些断断续续的台阶,如图是其中的甲、乙段台阶路的示意图,图8中的数字表示每一级台阶的高度(单位:cm).并且数d、e、e、c、c、d的方差p,数据b、d、g、f、a、h的方差q,(10cm<a<b<c<d<e<f<g<h<20cm,且 p<q),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题: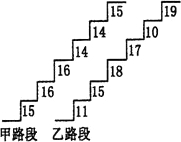 在某旅游景区上山的一条小路上,有一些断断续续的台阶.如图是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
在某旅游景区上山的一条小路上,有一些断断续续的台阶.如图是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题: