题目内容
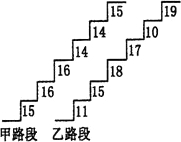 在某旅游景区上山的一条小路上,有一些断断续续的台阶.如图是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
在某旅游景区上山的一条小路上,有一些断断续续的台阶.如图是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服,为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
(图中的数字表示每一级台阶的高度(单位:cm).并且数据15,16,16,14,14,15的方差S甲2=
| 2 |
| 3 |
| 35 |
| 3 |
分析:(1)分别求出甲、乙的中位数、方差和极差进而分析得出即可;
(2)根据方差的性质得出即可;
(3)根据方差的稳定性得出即可.
(2)根据方差的性质得出即可;
(3)根据方差的稳定性得出即可.
解答:解:(1)∵从小到大排列出台阶的高度值:甲的,14,14,15,15,16,16,乙的,10,11,15,17,18,19,
甲的中位数、方差和极差分别为,15cm;
;16-14=2(cm),
乙的中位数、方差和极差分别为,(15+17)÷2=16(cm),
,19-10=9(cm)
平均数:
=
(15+16+16+14+14+15)=15(cm);
∴
=
(11+15+18+17+10+19)=15(cm).
∴相同点:两段台阶路高度的平均数相同.
不同点:两段台阶路高度的中位数、方差和极差均不相同.
(2)甲路段走起来更舒服一些,因为它的台阶高度的方差小.
(3)每个台阶高度均为15cm(原平均数),使得方差为0.
甲的中位数、方差和极差分别为,15cm;
| 2 |
| 3 |
乙的中位数、方差和极差分别为,(15+17)÷2=16(cm),
| 35 |
| 3 |
平均数:
. |
| x甲 |
| 1 |
| 6 |
∴
. |
| x乙 |
| 1 |
| 6 |
∴相同点:两段台阶路高度的平均数相同.
不同点:两段台阶路高度的中位数、方差和极差均不相同.
(2)甲路段走起来更舒服一些,因为它的台阶高度的方差小.
(3)每个台阶高度均为15cm(原平均数),使得方差为0.
点评:本题考查了样本中的平均数,方差,极差,中位数在生活中的意义和应用.

练习册系列答案
相关题目


 ,数据11,15,18,17,10,19的方差S乙2=
,数据11,15,18,17,10,19的方差S乙2= 。
。
 ,数据11,15,18,17,10,19的方差S乙2=
,数据11,15,18,17,10,19的方差S乙2= ).
).