��Ŀ����
����Ŀ����֪��O����O��һ��P��
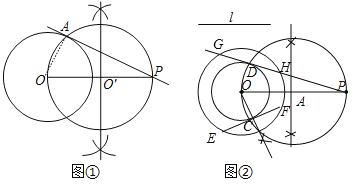
��1������֤���������ֱ�ߺ�Բ�����P����O��һ�������أ�С���������ͼ����ʾ�ķ�����
������OP����OPΪֱ������O����
�ڡ�O�����O�ཻ�ڵ�A����ֱ��PA��
��ֱ��PA��Ϊ�����Ĺ���P�ġ�O��һ�����ߣ�
��֤��С����ͼ��������ȷ�ԣ�
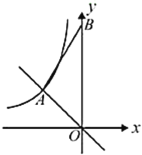
��2������Ǩ�ƣ���ͼ�ڣ���֪�߶�l������P��һ��ֱ�����O�ཻ���Ҹ�ֱ�߱���O���صõ��ҳ�����l����������ͼ�ۼ�����Ҫ��д������֤����

���𰸡���1������������2��������
��������
��1������OA��ֻҪ֤��OA��PA���ɣ�
��2���ڴ�Բ��O��ȡ��E����ȡEF=�߶�l������Բ��O�ڵ�F����EF�Ĵ�ֱƽ����OC������ΪC���Ե�OΪԲ�ģ�OCΪ�뾶��СԲ��O������OP����OPΪֱ����Բ��A����СԲ��O�ڵ�D������OD��PD���ӳ���Q�����Բ��O���ڵ�G��H����OD��PD������ΪD����OD=OC���ɵ�GH=EF=�߶�l��
��1��֤������ͼ���У�����OA��
��OP��ֱ����
���OAP=90����
��OA��PA��
��PA����O�����ߣ�
��2���⣺�������ڴ�Բ��O��ȡ��E����ȡEF=�߶�l������Բ��O�ڵ�F��
��EF�Ĵ�ֱƽ����OC������ΪC��
�Ե�OΪԲ�ģ�OCΪ�뾶��СԲ��O��
����OP����OPΪֱ����Բ��A��
��СԲ��O�ڵ�D��
����OD��PD���ӳ���Q�����Բ��O���ڵ�G��H��
��ΪOP����A��ֱ����
������PDO=90������OD��PD������ΪD��
��OD=OC��
��GH=EF=�߶�l��

 ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�