题目内容
【题目】如图![]() 、图
、图![]() 、图
、图![]() ,在矩形
,在矩形![]() 中,
中,![]() 是
是![]() 边上的一点,以
边上的一点,以![]() 为边作平行四边形
为边作平行四边形![]() ,使点
,使点![]() 在
在![]() 的对边
的对边![]() 上,
上,
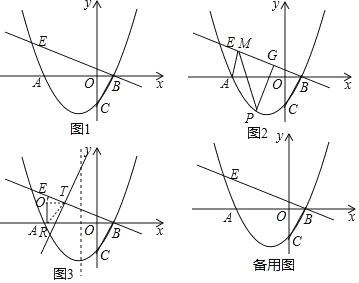
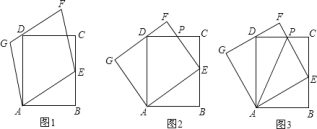
![]() 如图
如图![]() ,试说明:平行四边形
,试说明:平行四边形![]() 的面积与矩形
的面积与矩形![]() 的面积相等;
的面积相等;
![]() 如图
如图![]() ,若平行四边形
,若平行四边形![]() 是矩形,
是矩形,![]() 与
与![]() 交于点
交于点![]() ,试说明:
,试说明:![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一个圆上;
四点在同一个圆上;
![]() 如图
如图![]() ,若
,若![]() ,平行四边形
,平行四边形![]() 是正方形,且
是正方形,且![]() 是
是![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,判断以
,判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)见解析;(2)见解析;(3)以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切,理由见解析.
相切,理由见解析.
【解析】
(1)作出AE边上的高,分别得出长方形和平行四边形的面积表达式,可得其结果相同,从而说明平行四边形AEFG的面积与矩形ABCD的面积相等.
(2)先求出∠ADC=∠FEA=90°,再根据圆内接四边形的判定定理:“如果一个四边形的一组对角互补,那么这个四边形内接于圆”解答.
(3)过D作DH⊥AP于H,根据∠2+∠3=90°,∠1+∠2=90°,可得∠3=∠1,可求出△ADG∽△AEB;再根据D是FG的中点可求出其相似比为2,再由△ADG与△AEB相似可得其对应边成比例,可求出△ADG∽△AEB∽△APD;最后根据相似三角形的性质可得AD是∠GAH的平分线,可求出DG=DH,故DG=DF,即可解答.
![]() 过
过![]() 点作
点作![]() 垂直
垂直![]() 于点
于点![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
所以![]() ,
,
所以,![]() .
.
![]() 因为平行四边形
因为平行四边形![]() 是矩形,四边形
是矩形,四边形![]() 也是矩形;
也是矩形;
所以![]() ,
,
则![]() ,
,
所以![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一个圆上.
四点在同一个圆上.
![]() 相切.
相切.
过![]() 作
作![]() 于
于![]() ;
;
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
在![]() 与
与![]() 中,
中,![]() ;
;
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() 是
是![]() 的平分线,
的平分线,
∴![]() ,∵
,∵![]() ,
,![]() ,
,
∴以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.

练习册系列答案
相关题目