ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷Σ»γΆΦΘ§≈ΉΈοœΏy=![]() x2+
x2+![]() x©¹
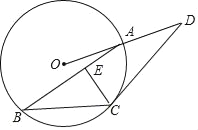
x©¹![]() ”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©”κy÷αΫΜ”ΎΒψCΘ§÷±œΏBEΓΆBC”κΒψBΘ§”κ≈ΉΈοœΏΒΡΝμ“ΜΫΜΒψΈΣEΘ°
”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©”κy÷αΫΜ”ΎΒψCΘ§÷±œΏBEΓΆBC”κΒψBΘ§”κ≈ΉΈοœΏΒΡΝμ“ΜΫΜΒψΈΣEΘ°
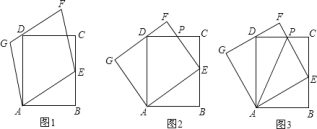
Θ®1Θ©»γΆΦ1Θ§«σΒψEΒΡΉχ±ξΘΜ
Θ®2Θ©»γΆΦ2Θ§»τΒψPΈΣx÷αœ¬ΖΫ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§ΙΐPΉςPGΓΆBE”κΒψGΘ§Β±PG≥ΛΕ»Ήν¥σ ±Θ§‘Ύ÷±œΏBE…œ’““ΜΒψMΘ§ ΙΒΟΓςAPMΒΡ÷ή≥ΛΉν–ΓΘ§≤Δ«σ≥ω÷ή≥ΛΒΡΉν–Γ÷ΒΘ°
Θ®3Θ©»γΆΦ3Θ§ΫΪΓςBOC‘Ύ…δœΏBE…œΘ§…ηΤΫ“ΤΚσΒΡ»ΐΫ«–ΈΈΣΓςBΓδOΓδCΓδΘ§BΓδ‘Ύ…δœΏBE…œΘ§»τ÷±œΏBΓδCΓδΖ÷±π”κx÷αΓΔ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΫΜ”ΎΒψRΓΔTΘ§Β±ΓςOΓδRTΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§«σRΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©EΘ®©¹4Θ§![]() Θ©ΘΜΘ®2Θ©
Θ©ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©RΘ®
ΘΜΘ®3Θ©RΘ®![]() Θ§0Θ©ΜρΘ®
Θ§0Θ©ΜρΘ®![]() Θ§0Θ©ΜρΘ®
Θ§0Θ©ΜρΘ®![]() Θ§0Θ©ΜρΘ®
Θ§0Θ©ΜρΘ®![]() Θ§0Θ©Θ°
Θ§0Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©«σ≥ω÷±œΏBEΒΡΫβΈω ΫΘ§άϊ”ΟΖΫ≥ΧΉι«σ≥ωΫΜΒψEΉχ±ξΘΜ
Θ®2Θ©»γΆΦ2÷–Θ§ΉςPKΓΈOCΫΜBE”ΎKΘ°“ρΈΣΓœPKB «Ε®÷Β=60ΓψΘ§ΆΤ≥ωΒ±PKΒΡ÷ΒΉν¥σ ±Θ§PGΒΡ÷ΒΉν¥σΘ§…ηPΘ®mΘ§![]() m2+
m2+![]() m©¹
m©¹![]() Θ©Θ§‘ρKΘ®mΘ§©¹
Θ©Θ§‘ρKΘ®mΘ§©¹![]() m+
m+![]() Θ©Θ§Ω…ΒΟPK=©¹
Θ©Θ§Ω…ΒΟPK=©¹![]() m2©¹
m2©¹![]() m+
m+![]() Θ§Ω…÷ΣΒ±m=©¹
Θ§Ω…÷ΣΒ±m=©¹![]() ±Θ§PKΒΡ÷ΒΉν¥σΘ§¥Υ ±PΘ®©¹
±Θ§PKΒΡ÷ΒΉν¥σΘ§¥Υ ±PΘ®©¹![]() Θ§©¹
Θ§©¹![]() Θ©Θ°»γΆΦ2©¹1÷–Θ§ΉςAΙΊ”ΎBEΒΡΕ‘≥ΤΒψAΓδΘ§Ν§Ϋ”PAΓδΫΜBE”ΎMΘ§Ν§Ϋ”AMΓΔAPΘ§¥Υ ±ΓςPAMΒΡ÷ή≥ΛΉν–ΓΘΜ
Θ©Θ°»γΆΦ2©¹1÷–Θ§ΉςAΙΊ”ΎBEΒΡΕ‘≥ΤΒψAΓδΘ§Ν§Ϋ”PAΓδΫΜBE”ΎMΘ§Ν§Ϋ”AMΓΔAPΘ§¥Υ ±ΓςPAMΒΡ÷ή≥ΛΉν–ΓΘΜ
Θ®3Θ©»γΆΦ3÷–Θ§…ηBBΓδ=![]() mΘ§‘ρBR=2mΘ§RΘ®1©¹2mΘ§0Θ©Θ§OΓδΘ®©¹
mΘ§‘ρBR=2mΘ§RΘ®1©¹2mΘ§0Θ©Θ§OΓδΘ®©¹![]() mΘ§
mΘ§![]() mΘ©Θ§Ζ÷»ΐ÷÷«ι–ΈΔΌΒ±OΓδT=RT ±ΘΜΔΎΒ±OΓδT=OΓδR ±ΘΜΔέΒ±RT=ROΓδ ±Θ§Ζ÷±πΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ Χβ.
mΘ©Θ§Ζ÷»ΐ÷÷«ι–ΈΔΌΒ±OΓδT=RT ±ΘΜΔΎΒ±OΓδT=OΓδR ±ΘΜΔέΒ±RT=ROΓδ ±Θ§Ζ÷±πΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ Χβ.
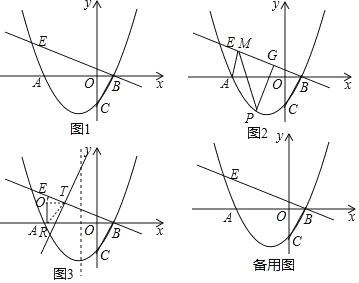
Θ®1Θ©ΓΏ≈ΉΈοœΏy=![]() x2+
x2+![]() x©¹
x©¹![]() ”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©”κy÷αΫΜ”ΎΒψCΘ§
”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©”κy÷αΫΜ”ΎΒψCΘ§
Ννy=0Θ§ΒΟΒΫ![]() x2+
x2+![]() x©¹
x©¹![]() =0Θ§ΫβΒΟx=©¹3Μρ1Θ§
=0Θ§ΫβΒΟx=©¹3Μρ1Θ§
ΓύAΘ®©¹3Θ§0Θ©Θ§BΘ®1Θ§0Θ©Θ§
Ννx=0Θ§ΒΟΒΫy=©¹![]() Θ§
Θ§
ΓύCΘ®0Θ§©¹![]() Θ©Θ§
Θ©Θ§
Γύ÷±œΏBCΒΡΫβΈω ΫΈΣy=![]() x©¹
x©¹![]() Θ§
Θ§
ÿBEâBCȧ
Γύ÷±œΏBEΒΡΫβΈω ΫΈΣy=©¹![]() x+
x+![]() Θ§
Θ§
”… Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Μρ
Μρ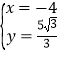 Θ§
Θ§
ΓύEΘ®©¹4Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Θ®2Θ©»γΆΦ2÷–Θ§ΉςPKΓΈOCΫΜBE”ΎKΘ°

ΓΏΓœPKB «Ε®÷Β=60ΓψΘ§
ΓύΒ±PKΒΡ÷ΒΉν¥σ ±Θ§PGΒΡ÷ΒΉν¥σΘ§…ηPΘ®mΘ§![]() m2+
m2+![]() m©¹
m©¹![]() Θ©Θ§‘ρKΘ®mΘ§©¹
Θ©Θ§‘ρKΘ®mΘ§©¹![]() m+
m+![]() Θ©Θ§
Θ©Θ§
ΓύPK=©¹![]() m2©¹
m2©¹![]() m+
m+![]() Θ§
Θ§
ΓΏ©¹![]() ΘΦ0Θ§
ΘΦ0Θ§
ΓύΒ±m=©¹![]() ±Θ§PKΒΡ÷ΒΉν¥σΘ§¥Υ ±PΘ®©¹
±Θ§PKΒΡ÷ΒΉν¥σΘ§¥Υ ±PΘ®©¹![]() Θ§©¹
Θ§©¹![]() Θ©Θ°
Θ©Θ°
»γΆΦ2©¹1÷–Θ§ΉςAΙΊ”ΎBEΒΡΕ‘≥ΤΒψAΓδΘ§Ν§Ϋ”PAΓδΫΜBE”ΎMΘ§Ν§Ϋ”AMΓΔAPΘ§¥Υ ±ΓςPAMΒΡ÷ή≥ΛΉν–ΓΘ§
ΓΏAΘ®©¹3Θ§0Θ©Θ§Ω…ΒΟAΓδΘ®©¹1Θ§2![]() Θ©Θ§
Θ©Θ§
ΓύΓςPAMΒΡ÷ή≥ΛΒΡΉν–Γ÷Β=PM+MA+PA=PA+PM+MAΓδ=PA+PAΓδ=![]() +
+![]() =
=![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦ3÷–Θ§…ηBBΓδ=![]() mΘ§‘ρBR=2mΘ§RΘ®1©¹2mΘ§0Θ©Θ§OΓδΘ®©¹
mΘ§‘ρBR=2mΘ§RΘ®1©¹2mΘ§0Θ©Θ§OΓδΘ®©¹![]() mΘ§
mȧ![]() mȩȧ
mΘ©Θ§

…η÷±œΏBBΓδΒΡΫβΈω ΫΈΣy=![]() x+bΘ§Α―RΘ®1©¹2mΘ§0Θ©¥ζ»κΘ§ΒΟΒΫb=
x+bΘ§Α―RΘ®1©¹2mΘ§0Θ©¥ζ»κΘ§ΒΟΒΫb=![]() Θ®2m©¹1Θ©Θ§
Θ®2m©¹1Θ©Θ§
Γύ÷±œΏBΓδCΓδΒΡΫβΈω ΫΈΣy=![]() x+
x+![]() Θ®2m©¹1Θ©Θ§
Θ®2m©¹1Θ©Θ§
ΓύTΘ®©¹1Θ§2![]() m©¹2
m©¹2![]() Θ©Θ§
Θ©Θ§
ΓύOΓδR2=Θ®![]() m©¹1Θ©2+Θ®
m©¹1Θ©2+Θ®![]() mΘ©2Θ§OΓδT2=Θ®1©¹
mΘ©2Θ§OΓδT2=Θ®1©¹![]() mΘ©2+Θ®2
mΘ©2+Θ®2![]() ©¹
©¹![]() mΘ©2Θ§RT2=Θ®2©¹2mΘ©2+Θ®2
mΘ©2Θ§RT2=Θ®2©¹2mΘ©2+Θ®2![]()
![]() ©¹2
©¹2![]() mΘ©2Θ§
mΘ©2Θ§
ΔΌΒ±OΓδT=RT ±Θ§Θ®1©¹![]() mΘ©2+Θ®2
mΘ©2+Θ®2![]() ©¹
©¹![]() mΘ©2=Θ®2©¹2mΘ©2+Θ®2
mΘ©2=Θ®2©¹2mΘ©2+Θ®2![]() ©¹2
©¹2![]() mΘ©2Θ§
mΘ©2Θ§
’ϊάμΒΟΘΚ7m2©¹11m+3=0Θ§
ΫβΒΟm=![]() Θ§
Θ§
ΓύRΘ®![]() Θ§0Θ©ΜρΘ®
Θ§0Θ©ΜρΘ®![]() Θ§0Θ©Θ°
Θ§0Θ©Θ°
ΔΎΒ±OΓδT=OΓδR ±Θ§Θ®![]() m©¹1Θ©2+Θ®
m©¹1Θ©2+Θ®![]() mΘ©2=Θ®1©¹
mΘ©2=Θ®1©¹![]() mΘ©2+Θ®2
mΘ©2+Θ®2![]() ©¹
©¹![]() mΘ©2Θ§
mΘ©2Θ§
’ϊάμΒΟΘΚ2m2©¹5m+6=0Θ§
ΓςΘΦ0ΈόΫβΘ°
ΔέΒ±RT=ROΓδ ±Θ§Θ®![]() m©¹1Θ©2+Θ®
m©¹1Θ©2+Θ®![]() mΘ©2=Θ®2©¹2mΘ©2+Θ®2
mΘ©2=Θ®2©¹2mΘ©2+Θ®2![]() ©¹2
©¹2![]() mΘ©2Θ§
mΘ©2Θ§
’ϊάμΒΟ15m2©¹31m+15=0
ΫβΒΟm=![]() Θ§
Θ§
ΓύRΘ®![]() Θ§0Θ©ΜρΘ®
Θ§0Θ©ΜρΘ®![]() Θ§0Θ©Θ°
Θ§0Θ©Θ°

ΓΨΧβΡΩΓΩ ΓΑ…Ά÷–ΜΣ Ϊ¥ Θ§―ΑΈΡΜ·Μυ“ρΘ§ΤΖ…ζΜν÷°ΟάΓ±Θ§Ρ≥–ΘΨΌΑλΝΥ ΉΫλΓΑ÷–Ιζ Ϊ¥ ¥σΜαΓ±Θ§Ψ≠―ΓΑΈΚσ”–50Οϊ―ß…ζ≤ΈΦ”Ψω»ϋΘ§’β50Οϊ―ß…ζΆ§ ±Ρ§–¥50 ΉΙ≈ Ϊ¥ Θ§»τΟΩ’ΐ»ΖΡ§–¥≥ω“Μ ΉΙ≈ Ϊ¥ ΒΟ2Ζ÷Θ§ΗυΨί≤β ‘≥…Φ®Μφ÷Τ≥ω≤ΩΖ÷ΤΒ ΐΖ÷≤Φ±μΚΆ≤ΩΖ÷ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ»γΆΦ±μΘΚ
«κΫαΚœΆΦ±μΆξ≥…œ¬Ν–ΗςΧβΘΚ
Θ®1Θ©ΔΌ±μ÷–aΒΡ÷ΒΈΣ Θ§÷–ΈΜ ΐ‘ΎΒΎ ΉιΘΜ
ΔΎΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®2Θ©»τ≤β ‘≥…Φ®≤ΜΒΆ”Ύ80Ζ÷ΈΣ”≈–ψΘ§‘ρ±Ψ¥Έ≤β ‘ΒΡ”≈–ψ¬ «Εύ…ΌΘΩ
Θ®3Θ©ΒΎ5Ήι10ΟϊΆ§―ß÷–Θ§”–4ΟϊΡ–Ά§―ßΘ§œ÷ΫΪ’β10ΟϊΆ§―ßΤΫΨυΖ÷≥…ΝΫΉιΫχ––Ε‘ΩΙΝΖœΑΘ§«“4ΟϊΡ–Ά§―ßΟΩΉιΖ÷ΝΫ»ΥΘ§«σ–ΓΟς”κ–Γ«ΩΝΫΟϊΡ–Ά§―ßΡήΖ÷‘ΎΆ§“ΜΉιΒΡΗ≈¬ Θ°
Ήι±π | ≥…Φ®xΖ÷ | ΤΒ ΐΘ®»Υ ΐΘ© |
ΒΎ1Ήι | 50ΓήxΘΦ60 | 6 |
ΒΎ2Ήι | 60ΓήxΘΦ70 | 8 |
ΒΎ3Ήι | 70ΓήxΘΦ80 | 14 |
ΒΎ4Ήι | 80ΓήxΘΦ90 | a |
ΒΎ5Ήι | 90ΓήxΘΦ100 | 10 |