题目内容
【题目】如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
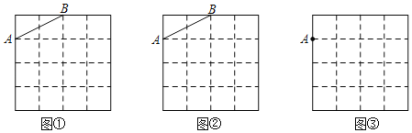
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形ABC;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形,这个正方形的面积= .
【答案】10
【解析】
(1)根据勾股定理,结合网格结构。以B为圆心,AB长为半径画圆,可以画出3个;以A为圆心,AB长为半径画圆,可以画出2个
(2)根据勾股定理逆定理,结合网格结构,作出边长为![]() 的正方形;
的正方形;
(3)根据勾股定理逆定理,结合网格结构,作出最长的线段作为正方形的边长即可.
(1)如图①,符合条件的C点有5个: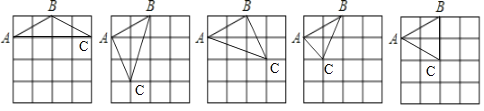 ;
;
(2)如图②,正方形ABCD即为满足条件的图形: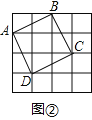 ;
;
(3)如图③,边长为![]() 的正方形ABCD的面积最大.
的正方形ABCD的面积最大.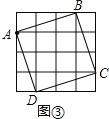 .
.
此时正方形的面积为(![]() )2=10,
)2=10,
故答案为:10.

练习册系列答案
相关题目