题目内容
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=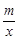 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=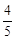 .
.
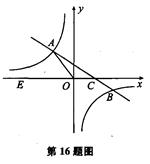
小题1:求该反比例函数和一次函数的解析式
小题2:求△AOC的面积
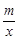 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=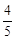 .
.
小题1:求该反比例函数和一次函数的解析式
小题2:求△AOC的面积
小题1:y=-
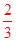 x+2;
x+2;小题2:6
:(1)过点A作AD⊥x轴于D点,如图,
∵sin∠AOE=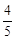 ,OA=5,
,OA=5,
∴sin∠AOE=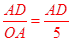 =
=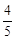 ,
,
∴AD=4,
∴DO=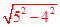 =3,
=3,
而点A在第二象限,
∴点A的坐标为(-3,4),
将A(-3,4)代入y=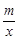 ,得m=-12,
,得m=-12,
∴反比例函数的解析式为y=-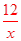 ;
;
将B(6,n)代入y=-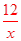 ,得n=-2;
,得n=-2;
将A(-3,4)和B(6,-2)分别代入y=kx+b(k≠0),得
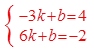 ,
,
解得,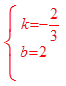
∴所求的一次函数的解析式为y=-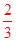 x+2;
x+2;
(2)在y=-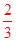 x+2中,令y=0,
x+2中,令y=0,
即-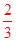 x+2=0,
x+2=0,
解得x=3,
∴C点坐标为(3,0),即OC=3,
∴S△AOC=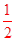 •AD•OC=
•AD•OC=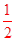 •4•3=6.
•4•3=6.
∵sin∠AOE=
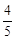 ,OA=5,
,OA=5,∴sin∠AOE=
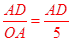 =
=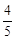 ,
,∴AD=4,
∴DO=
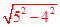 =3,
=3,而点A在第二象限,
∴点A的坐标为(-3,4),
将A(-3,4)代入y=
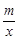 ,得m=-12,
,得m=-12,∴反比例函数的解析式为y=-
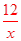 ;
;将B(6,n)代入y=-
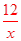 ,得n=-2;
,得n=-2;将A(-3,4)和B(6,-2)分别代入y=kx+b(k≠0),得
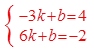 ,
,解得,
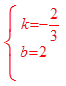
∴所求的一次函数的解析式为y=-
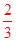 x+2;
x+2;(2)在y=-
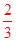 x+2中,令y=0,
x+2中,令y=0,即-
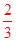 x+2=0,
x+2=0,解得x=3,
∴C点坐标为(3,0),即OC=3,
∴S△AOC=
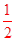 •AD•OC=
•AD•OC=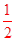 •4•3=6.
•4•3=6.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
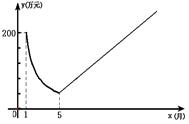
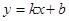 与反比例函数
与反比例函数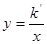 (
( <0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.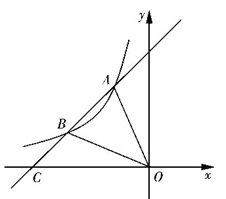
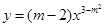 是反比例函数.
是反比例函数. )、B(-1,y
)、B(-1,y )、C(3,y
)、C(3,y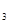 )都在反比例函数y=
)都在反比例函数y=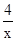 的图象上,则( )
的图象上,则( )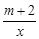 的图象在其象限内y的值随x值的增大而增大,则m的取值范围是 ( )
的图象在其象限内y的值随x值的增大而增大,则m的取值范围是 ( ) 的图象上,则下列结论中正确的是( )
的图象上,则下列结论中正确的是( )
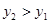

 的图像与反比例函数
的图像与反比例函数 的图像有一个交点的横坐标是
的图像有一个交点的横坐标是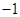 ,那么它们的交点坐标分别为_______.
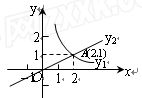
,那么它们的交点坐标分别为_______.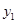 与正比例函数y2的图象的一个交点坐标是A(2,1),若y2>y1>0,则x的取值范围在数轴上表示为( )
与正比例函数y2的图象的一个交点坐标是A(2,1),若y2>y1>0,则x的取值范围在数轴上表示为( )