Question

【题目】在平面直角坐标系中，O为原点，点A（8，0）、点B（0，4），点C、D分别是边OA、AB的中点．将△ACD绕点A顺时针方向旋转，得△AC′D′，记旋转角为α．

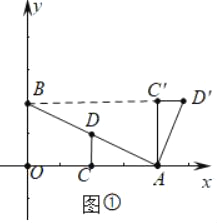
（I）如图①，连接BD′，当BD′∥OA时，求点D′的坐标；

（II）如图②，当α=60°时，求点C′的坐标；

（III）当点B，D′，C′共线时，求点C的坐标（直接写出结果即可）．

Answer 1

【答案】（I）（10，4）或（6，4）（II）C′（6，2）（III）①C′（8，4）②

C′（，﹣）

【解析】

（I）如图①，当OB∥AC′，四边形OBC′A是平行四边形，只要证明B、C′、D′共线即可解决问题，再根据对称性确定D″的坐标；

（II）如图②，当α=60°时，作C′K⊥AC于K．解直角三角形求出OK，C′K即可解决问题；

（III）分两种情形分别求解即可解决问题；

解:（I）如图①，

∵A（8，0），B（0，4），

∴OB=4，OA=8，

∵AC=OC=AC′=4，

∴当OB∥AC′，四边形OBC′A是平行四边形，

∵∠AOB=90°，

∴四边形OBC′A是矩形，

∴∠AC′B=90°，∵∠AC′D′=90°，

∴B、C′、D′共线，

∴BD′∥OA，

∵AC=CO， BD=AD，

∴CD=C′D′=OB=2，

∴D′（10，4），

根据对称性可知，点D″在线段BC′上时，D″（6，4）也满足条件．

综上所述，满足条件的点D坐标（10，4）或（6，4）．

（II）如图②，当α=60°时，作C′K⊥AC于K．

在Rt△AC′K中，∵∠KAC′=60°，AC′=4，

∴AK=2，C′K=2，

∴OK=6，

∴C′（6，2）．

（III）①如图③中，当B、C′、D′共线时，由（Ⅰ）可知，C′（8，4）．

②如图④中，当B、C′、D′共线时，BD′交OA于F，易证△BOF≌△AC′F，

∴OF=FC′，设OF=FC′=x，

在Rt△ABC′中，BC′==8，

在RT△BOF中，OB=4，OF=x，BF=8﹣x，

∴（8﹣x）2=42+x2，

解得x=3，

∴OF=FC′=3，BF=5，作C′K⊥OA于K，

∵OB∥KC′，

∴==，

∴==，

∴KC′=，KF=，

∴OK=，

∴C′（，﹣）．