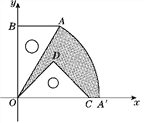
[题目]如图.在中..点在轴上.点坐标为.(1)求点到轴的距离,(2)连接.当时.求点的坐标,(3)在(2)的条件下.猜想线段和线段的数量关系.并说明理由. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在中，，点在轴上，点坐标为。

（1）求点到轴的距离；

（2）连接，当时，求点的坐标；

（3）在（2）的条件下，猜想线段和线段的数量关系，并说明理由。

【答案】（1）2；（2）的坐标为；（3），理由见解析

【解析】

（1）作辅助线，过点作轴，于点.通过证明根据全等的性质得到，即可知到轴的距离.

（2）作辅助线过点作轴于点，求出，进而得到，即可求出的坐标.

（3）利用全等的性质可得：，再求出OB的长度，即可得到与的关系.

（1）过点作轴，于点.

∵，

∴

∵轴

∵

在与中

∴

∴到轴的距离为2.

（2）过点作轴于点

∴

∵

∴

∴的坐标为

（3）与的关系为

∵坐标为，D点坐标（0,2）

∴BD=2-(-2)=4，OB=2

∵（已证）

∴

又∵OB=2

∴.

练习册系列答案

相关题目

【题目】如图，在四边形ABCD中，AD∥BC，∠B=90°，BC=6，AD=3，AB=，点E，F同时从B点出发，沿射线BC向右匀速移动，已知点F的移动速度是点E移动速度的2倍，以EF为一边在CB的上方作等边△EFG，设E点移动距离为x（0＜x＜6）．

（1）∠DCB=　　度，当点G在四边形ABCD的边上时，x=　　；

（2）在点E，F的移动过程中，点G始终在BD或BD的延长线上运动，求点G在线段BD的中点时x的值；

（3）当2＜x＜6时，求△EFG与四边形ABCD重叠部分面积y与x之间的函数关系式，当x取何值时，y有最大值？并求出y的最大值．

【题目】在△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、BC于D、E．若∠CAB=∠B+30°，CE=2cm．

求:（1）∠AEB 度数．

（2）BC的长．

【题目】在平面直角坐标系中，O为原点，点A（8，0）、点B（0，4），点C、D分别是边OA、AB的中点．将△ACD绕点A顺时针方向旋转，得△AC′D′，记旋转角为α．

（I）如图①，连接BD′，当BD′∥OA时，求点D′的坐标；

（II）如图②，当α=60°时，求点C′的坐标；

（III）当点B，D′，C′共线时，求点C的坐标（直接写出结果即可）．

【题目】今年5月19日为第29个“全国助残日”．我市某中学组织了献爱心捐款活动，该校数学课外活动小组对本次捐款活动做了一次抽样调查，并绘制了如下不完整的频数分布表和频数分布直方图（每组含前一个边界，不含后一个边界）．

（1）填空：_________，_________．

（2）补全频数分布直方图．

（3）该校有2000名学生，估计这次活动中爱心捐款额在的学生人数．

【题目】如图，有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把这两块三角板放置在平面直角坐标系中，且OB＝3.

(1)若某反比例函数的图象的一个分支恰好经过点A，求这个反比例函数的解析式；

(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后，斜边OA恰好落在x轴上，点A落在点A′处，试求图中阴影部分的面积．(结果保留π)

【答案】(1)反比例函数的解析式为y＝；(2)S阴影＝6π－.

【解析】分析：（1）根据tan30°=，求出AB，进而求出OA，得出A的坐标，设过A的双曲线的解析式是y=，把A的坐标代入求出即可；（2）求出∠AOA′，根据扇形的面积公式求出扇形AOA′的面积，求出OD、DC长，求出△ODC的面积，相减即可求出答案．

本题解析：

(1)在Rt△OBA中，∠AOB＝30°，OB＝3，

∴AB＝OB·tan 30°＝3.

∴点A的坐标为(3，3)．

设反比例函数的解析式为y＝ (k≠0)，

∴3＝，∴k＝9，则这个反比例函数的解析式为y＝.

(2)在Rt△OBA中，∠AOB＝30°，AB＝3，

sin ∠AOB＝，即sin 30°＝，

∴OA＝6.

由题意得：∠AOC＝60°，S扇形AOA′＝＝6π.

在Rt△OCD中，∠DOC＝45°，OC＝OB＝3，

∴OD＝OC·cos 45°＝3×＝.

∴S△ODC＝OD2＝＝.

∴S阴影＝S扇形AOA′－S△ODC＝6π－.

点睛：本题考查了勾股定理、待定系数法求函数解析式、特殊角的三角函数值、扇形的面积及等腰三角形的性质，本题属于中档题，难度不大，将不规则的图形的面积表示成多个规则图形的面积之和是解答本题的关键.

【题型】解答题
【结束】
26

【题目】矩形ABCD一条边AD＝8，将矩形ABCD折叠，使得点B落在CD边上的点P处．

(1)如图①，已知折痕与边BC交于点O，连接AP，OP，OA.

① 求证：△OCP∽△PDA；

② 若△OCP与△PDA的面积比为1:4，求边AB的长．

(2)如图②，在(1)的条件下，擦去AO和OP，连接BP.动点M在线段AP上(不与点P，A重合)，动点N在线段AB的延长线上，且BN＝PM，连接MN交PB于点F，作ME⊥BP于点E.试问动点M，N在移动的过程中，线段EF的长度是否发生变化？若不变，求出线段EF的长度；若变化，说明理由．

【题目】某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况，随机抽取一部分学生进行问卷调查，统计整理并绘制了以下两幅不完整的统计图：

请根据以上统计图提供的信息，解答下列问题：

（1）共抽取　　名学生进行问卷调查；

（2）补全条形统计图，求出扇形统计图中“足球”所对应的圆心角的度数；

（3）该校共有3000名学生，请估计全校学生喜欢足球运动的人数．

（4）甲乙两名学生各选一项球类运动，请求出甲乙两人选同一项球类运动的概率．

【题目】一艘轮船在静水中的最大航速为20千米/时，它沿江以最大航速顺流航行100千米所用时间，与以最大航速逆流航行60千米所用时间相等，江水的流速为多少？

（1）设江水的流速为千米/时，填空：轮船顺流航行速度为_________千米/时，逆流航行速度为_________千米/时，顺流航行100千米所用时间为_________小时，逆流航行60千米所用时间为_________小时.

（2）列出方程，并求出问题的解.

【题目】为发展我市旅游经济，丹东天桥沟景区对门票采用动态的售票方法吸引游客，规定：门票定价为100元/人，非节假日打折售票，节假日按团队人数分段定价售票，即10人以下（含10人）的团队按原价售票；超过10人的团队，其中10人仍按原价售票，超过10人部分的游客打折售票。设某旅游团人数为人，非节假日购票款为（元），节假日购票款为（元），、与之间的函数图象如图所示.

（1）观察图象可知：_______，__________；

（2）直接写出和的函数关系式（不需要写出自变量的取值范围）；

（3）导游小王10月1日带团，10月20日（非节假日）带团都到天桥沟景区旅游，共付门票款4600元，、两个团队合计60人，求、两个团队各有多少人？

试题分类