Question

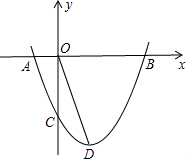
抛物线的顶点是C（2，

3

），它与x轴交于A、B两点，它们的横坐标是方程x²-4x+3=0的两个根，则AB=

 

，S_△ABC=

 

．

Answer 1

分析：首先，因为A，B两点的横坐标是方程x²-4x+3=0的两个根，可得A，B两点的坐标，即可得AB的长度；
然后，根据点的坐标特征可得S_△ABC=

1

2

×AB×C的纵坐标=

1

2

×AB×

3

即可求得面积．

解答：解：根据题意，
解方程x²-4x+3=0得：
x₁=1，x₂=3，
∴A点的坐标为（1，0），B点的坐标为（3，0），
∴AB=2，
根据图象上点的坐标特征得：
S_△ABC=

1

2

×AB×C的纵坐标=

1

2

×2×

3

=

3

，
即S_△ABC=

3

；

点评：本题考查二次函数图象上点的坐标特征，同时做题时需要灵活运用题目中的已知条件．