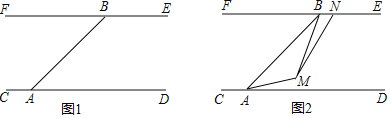Question

【题目】如图，在平面直角坐标系xOy中，AB∥OC，A（0，3），B（a，b），C（c，0），且a，c满足．点P从点A出发，以每秒1个单位长度的速度向点B运动，点Q从点O同时出发，以每秒2个单位长度的速度向点C运动，当点Q到达点C时，点P随之停止运动．设运动时间为t（秒）．

（1）B，C两点的坐标为：B ，C ；

（2）当t为何值时，四边形PQCB是平行四边形？

（3）D为线段AB的中点，求当t为何值时，△ADQ是等腰三角形？

Answer 1

【答案】（1），；（2）当t=4时，四边形PQCB是平行四边形；（3）当t为，或，或2，或时，△ADQ是等腰三角形．

【解析】

（1）根据点的坐标特点和二次根式的性质得出a，b，c的值进而得出答案；

（2）由题意得：，，根据平行四边形的判定可得再解方程即可；

（3）分别以AD为腰或AD为底边时情况，根据等腰三角形的性质和勾股定理即可得到结论．

解：（1）∵．

∴ ，

解得a=10，

∴c=14，

∵AB∥OC，A（0，3），

∴b=3，

即B（10，3），C（14，0）；

故答案为：（10，3），（14，0）

（2）设运动时间为t（秒），由题意可知：

，

又∵AB∥OC

∴当BP=CQ时，四边形PQCB是平行四边形

此时

解之得

∴当t=4时，四边形PQCB是平行四边形

（3）∵D为线段AB的中点

∴AD=5

分两种情况：①若AD为腰时，如图1：当DA=DQ=5时，△ADQ是等腰三角形

过点D作DE⊥OC

由题意可知D（5,3）

在Rt△DQE中，

∴OQ=5-4=1，即2t=1

∴

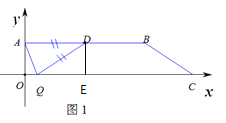
如图3：当AQ=AD=5时，△ADQ是等腰三角形

在Rt△AOQ中，OQ=4，即2t=4

∴

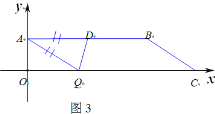
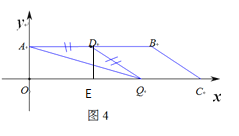
如图4：当DA=DQ时，△ADQ是等腰三角形

过点D作DE⊥OC

在Rt△DQE中，

∴OQ=5+4=9，即2t=9

∴

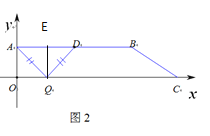
②若AD为底边，如图2：当QA=QD时，△ADQ是等腰三角形

过点Q作QE⊥AB，

∵AB∥OC，∠AOC=90°，QE⊥AB

∴∠∠AOC=∠OQE=∠QEA=90°

∴四边形OQEA是矩形

∴OQ=AE=

即，

∴

综上：当t为或2或或时，△ADQ是等腰三角形