题目内容
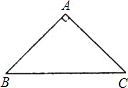 如图所示,△ABC为等腰直角三角形,斜边BC长为8.
如图所示,△ABC为等腰直角三角形,斜边BC长为8.
(1)建立适当的直角坐标系,并写出各个顶点的坐标;
(2)若△ABC各顶点的纵坐标不变,横坐标都加上2所得的三个点连成的三角形与原三角形有何关系?画图说明.
 解:如图所示.
解:如图所示.(1)以BC所在直线为x轴,BC的垂直平分线为y轴,建立直角坐标系.
∵△ABC是等腰直角三角形,BC=8,
∴OB=OC=OA=4,
∴A(0,4),B(-4,0),C(4,0).
(2)所得到的△A′B′C′与原三角形比较,原三角形向右平移了2个单位.
分析:(1)建立适当的直角坐标系,关键是确定原点的位置.
(2)△ABC各顶点的纵坐标不变,横坐标都加上2,将△ABC整体向右平移2个单位长度,原图形与新图形.
点评:考查直角坐标系的建立、平移变换的规律及等腰三角形的性质;理解平移变换不改变大小及形状是解答本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
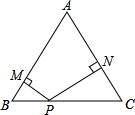 如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )
如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )A、
| ||||||
B、
| ||||||
C、80%<
| ||||||
D、78%<
|
 AE=120°,试问:
AE=120°,试问: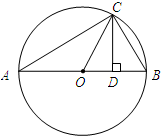 附加题.观察计算
附加题.观察计算 如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分.
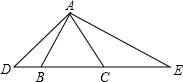
如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分. 如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=
如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=