题目内容
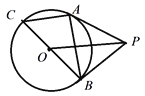
【题目】如图,P为⊙O外一点,PA、PB均为⊙O的切线,A和B是切点,BC是直径.
求证:(1)∠APB=2∠ABC;
(2)AC∥OP.
【答案】(1)证明见解析(2)见解析
【解析】
(1)连接OA, ∠OAP=∠OBP=90°,然后求出 PO垂直AB,从而导出∠APB=2∠ABC;
(2) 连接AB交PO于F,根据切线的性质得到PO垂直平分AB,再根据直径所对的圆周角是直角可得∠CAB=90°,于是∠CAB=∠OFB,所以AC∥OP.
(1)连接AO,
∵PA、PB均为⊙O的切线,A和B是切点,∴∠APO=∠BPO,OA⊥AP,PA=PB,
∴∠APB=2∠APO,∠OAP=90°,PO⊥AB,∴∠OAB+∠BAP=90°,∠BAP+∠APB=90°,
∴∠OAB=∠APB,∵OA=OB,∴∠OBA=∠OAB,∴∠OBA=∠APO,∴∠APB=2∠ABC;
(2)设AB交OP于F,∵PA,PB是圆的切线,∴PA=PB,∵OA=OB ∴PO垂直平分AB.
∴∠OFB=90°.∵BC是直径,∴∠CAB=90°.∴∠CAB=∠OFB.∴AC∥OP.

练习册系列答案
相关题目