Question

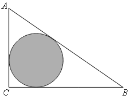
【题目】在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆与AB有何位置关系？(1) r=2cm；(2) r=2.4cm；(3) r=3cm．

Answer 1

【答案】（1）相离（2）相切（3）相交

【解析】

先根据题意画出图形,由勾股定理求出AB的长,作CD⊥AB于D,利用三角形的面积公式得出CD的长,再根据r的值与CD的大小进行解答.

∵∠C＝90°，AC＝3cm，BC＝4cm，∴AB＝5cm.

作CD⊥AB于D, 则 AC·BC＝ AB·CD, CD＝ cm.

(1) ∵CD＝2.4cm＞r＝2cm, ∴直线AB与⊙C相离.

(2) ∵CD＝2.4cm＝r＝2.4cm, ∴直线AB与⊙C相切.

(3) ∵CD＝2.4cm＜r＝3cm, ∴直线AB与⊙C相交.