Question

【题目】如图，已知在△ABC中，∠ABC与∠ACB的平分线交于点P．

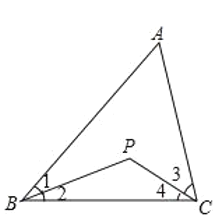
（1）当∠A=40°,∠ABC=60°时，求∠BPC的度数；

（2）当∠A=α°时，求∠BPC的度数．（用α的代数式表示）

Answer 1

【答案】（1）110°；（2）

【解析】

（1）根据三角形的内角和和角平分线的定义即可得到结论；
（2）先根据∠A=α，∠ABC与∠ACB的角平分线相交于P，求得∠PBC+∠PCB的度数，最后根据三角形内角和定理，求得∠BPC的度数；

（1）∵∠A=40°，∠ABC=60°，
∴∠ACB=80°，
∵∠ABC与∠ACB的平分线交于点P，
∴∠2=∠ABC=30°，∠4=∠ACB=40°，
∴∠BPC=180°-∠2-∠4=180°-30°-40°=110°；
（2）∵∠A=α，
∴∠ABC+∠ACB=180°-α，
∵∠ABC与∠ACB的角平分线相交于P，
∴∠PBC+∠PCB=（∠ABC+∠ACB）=×（180°-α），
在△PBC中，∠BPC=180°-（∠PBC+∠PCB）=180°-

×（180°-α）=90°+α；