题目内容
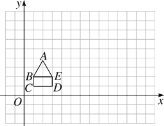
【题目】如图,△ABC与△DCE有公共顶点C,AB=CD,BC=CE,∠ABC=∠DCE=90°.
(1)如图1,当点D在BC延长线上时.
①求证:△ABC≌△DCE.
②判断AC与DE的位置关系,并说明理由.
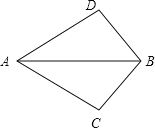
(2)如图2,△CDE从(1)中位置开始绕点C顺时针旋转,当点D落在BC边上时停止.
①若∠A=60°,记旋转的度数为![]() ,当
,当![]() 为何值时,DE与△ABC一边平行.
为何值时,DE与△ABC一边平行.
②如图3,若AB=c, BC=a, AC=b, a>c,边BC,DE交于点F,求整个运动过程中,F在BC上的运动路程(用含a, b, c的代数式表示)

【答案】(1)①见解析;②AC⊥DE,理由见解析;(2)①60°或90°或150°
②![]()
【解析】
(1)①由边角边可证全等;
②延长AC与DE交于M,由△ABC≌△DCE得∠ACB=∠E,利用等角的余角相等可证结论.
(2)①根据题意,作出符合条件的三种情况,易得旋转角度.
②根据题意,作出F的最终位置,即可得出运动路径.
(1)①证明:在△ABC和△DCE中,
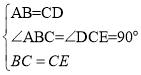
∴△ABC≌△DCE(SAS)
AC⊥DE,理由如下:
如图所示,延长AC与DE交于M,
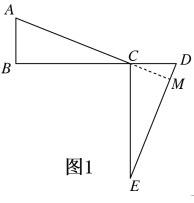
∵△ABC≌△DCE
∴∠ACB=∠E,
又∵∠ACB=∠DCM,∠E+∠D=90°
∴∠DCM+∠D=90°,
∴∠CMD=90°
即AC⊥DE.
(2)由题意可得,∠D=∠A=60°,∠E=∠ACB=30°,
(i)当DE∥BC时,如下图所示,
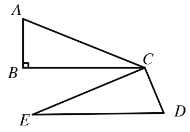
∵DE∥BC,
∴∠BCE=∠E=30°,
所以旋转角度![]() =90°-30°=60°
=90°-30°=60°
(ii)当DE∥AC时,如下图所示,此时BC和CE重合,
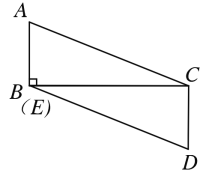
由图可知,![]() =∠BCD=90°
=∠BCD=90°
(iii)当DE∥AB时,如下图所示,
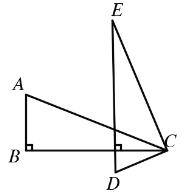
∵DE∥AB,AB⊥BC
∴DE⊥BC,
∴∠BCE=90°-30°=60°
∴![]() =90°+∠BCE=150°
=90°+∠BCE=150°
综上,![]() 为60°或90°或150°.
为60°或90°或150°.
②由题意可得,F点从B点开始运动到图1中![]() 点所示位置,然后再继续运动,返回到图2中F点重合,
点所示位置,然后再继续运动,返回到图2中F点重合,![]()
B点的运动路程为:![]()
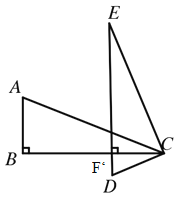
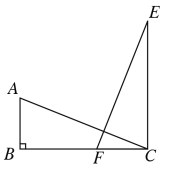
图1 图2

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案【题目】某市居民使用自来水按如下标准收费(水费按月缴纳)
月用水量 | 单价 |
不超过 |
|
超过 |
|
超过 |
|
(1)当![]() 时,某用户用了
时,某用户用了![]() 水,求该用户这个月应该缴纳的水费;
水,求该用户这个月应该缴纳的水费;
(2)设某用户用水量为![]() 立方米,求该用户应缴纳的水费(用含
立方米,求该用户应缴纳的水费(用含![]() 的式子表达)
的式子表达)