题目内容
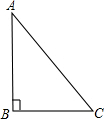 如图所示,△ABC为直角三角形,∠ABC=90°.
如图所示,△ABC为直角三角形,∠ABC=90°.(1)用尺规作图:做线段AB的垂直平分线l,垂足为H.(保留作图痕迹,不写作法);
(2)设直线l交AC于D,求证:AD•AB=AH•AC.
分析:(1)分别以A为端点,以大于AB/2长为半径,在线段两侧分别作弧;再以B为端点,仍以大于AB/2长为半径,在线段两侧分别作弧,并与已作两弧交于两点,过两点作一条直线,则为线段AB的垂直平分线;
(2)根据HD是AB的垂直平分线知,AH=BH,HD⊥AB,所以AH=
AB,HD是直角三角形ABC的中位线,利用中位线定理求得HD=
BC,∠AHD=∠ABC=90°从而证明△AHD∽△ABC(SAS);最后由相似三角形的对应边成比例来证明AD•AB=AH•AC.
(2)根据HD是AB的垂直平分线知,AH=BH,HD⊥AB,所以AH=
| 1 |
| 2 |
| 1 |
| 2 |
解答: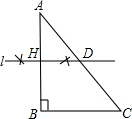 解:(1)AH=BH,HD⊥AB;
解:(1)AH=BH,HD⊥AB;
(2)证明:∵HD⊥AB,∠ABC=90°,
∴HD∥BC;
又∵AH=BH,
∴
=
=
;
在△AHD与△ABC中,
=
,
∠AHD=∠ABC=90°,
∴△AHD∽△ABC(SAS),
∴
=
(相似三角形的对应边成比例),
∴AD•AB=AH•AC.
 解:(1)AH=BH,HD⊥AB;
解:(1)AH=BH,HD⊥AB;(2)证明:∵HD⊥AB,∠ABC=90°,
∴HD∥BC;
又∵AH=BH,
∴
| AH |
| AB |
| HD |
| BC |
| 1 |
| 2 |
在△AHD与△ABC中,
| AH |
| AB |
| HD |
| BC |
∠AHD=∠ABC=90°,
∴△AHD∽△ABC(SAS),
∴
| AD |
| AC |
| AH |
| AB |
∴AD•AB=AH•AC.
点评:本题主要考查了相似三角形的判定与性质.解答此题时,利用了三角形的中位线定理、线段的垂直平分线的性质.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
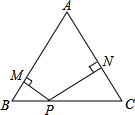 如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )
如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )A、
| ||||||
B、
| ||||||
C、80%<
| ||||||
D、78%<
|
 AE=120°,试问:
AE=120°,试问: 附加题.观察计算
附加题.观察计算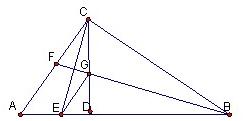 如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分.
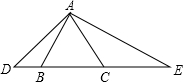
如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分. 如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=
如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=