题目内容
【题目】如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.
(1)求证:△AFN≌△CEM;
(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.

【答案】(1)证明见解析;(2)∠NAF=35°.
【解析】
(1)利用平行线的性质,根据SAS即可证明;
(2)利用全等三角形的性质可知∠NAF=∠ECM,求出∠ECM即可.
(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠AFN=∠CEM,
∵FN=EM,AF=CE,
∴△AFN≌△CEM(SAS).
(2)解:∵△AFN≌△CEM,
∴∠NAF=∠ECM,
∵∠CMF=∠CEM+∠ECM,
∴107°=72°+∠ECM,
∴∠ECM=35°,
∴∠NAF=35°.

练习册系列答案
相关题目
【题目】4月23日是“世界读书日”,某校文学社团随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:
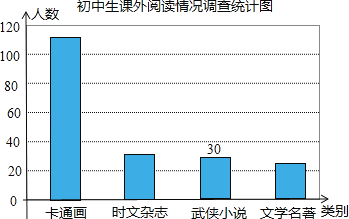
初中生课外阅读情况调查统计表
种类 | 频数 | 频率 |
卡通画 | a | 0.56 |
时文杂志 | 32 | b |
武侠小说 | c | 0.15 |
文学名著 | 26 | d |
(1)这次随机调查了几名学生?统计表中a,d各代表什么数值?
(2)试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍?
(3)结合以上统计数据,请你站在文学社团的立场发表一下你的看法.