题目内容
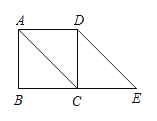
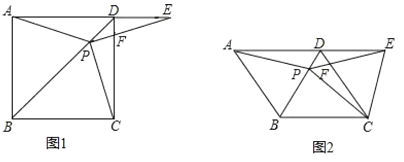
【题目】如图①,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PC=PE,PE交CD于点F.
(1)求证:∠PCD=∠PED;
(2)连接EC,求证:EC=![]() AP;
AP;
(3)如图②,把正方形ABCD改成菱形ABCD,其他条件不变,当∠DAB=60°时,请直接写出线段EC和AP的数量关系______.
【答案】(1)证明见解析;(2)证明见解析;(3)AP=CE.
【解析】
(1)根据正方形性质知道PC=PA,又由PE=PC知道PA=PE即可得出结论.
(2)证明△PEC为等腰直角三角形,即可得出结论.
(3)根据(2)的思路和方法即可求出结论AP=CE.
(1)证明:在正方形ABCD中,AD=DC,
∠ADP=∠CDP=45°,
在△ADP和△CDP中,AD=DC;∠ADP=∠CDP;PD=PD,
∴△ADP≌△CDP(SAS),
∴∠DAP=∠DCP,PA=PC;
∵PC=PE,
∴PA=PE,
∴∠DAP=∠DEP,
∴∠DCP=∠DAP=∠DEP.
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPF=∠EDF=90°;
∴△CPE是等腰直角三角形,
∴EC=![]() CP,
CP,
又∵AP=CP,
∴EC=![]() AP.
AP.
(3)AP=CE;理由如下:
在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,AB=BC;∠ABP=∠CBP;PB=PB,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP,
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.

 智慧小复习系列答案
智慧小复习系列答案【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 278 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计当![]() 很大时,摸到白球的频率将会接近 (精确到0.1);
很大时,摸到白球的频率将会接近 (精确到0.1);
(2)假如摸一次,摸到黑球的概率![]() ;
;
(3)试估算盒子里黑颜色的球有多少只.