Question

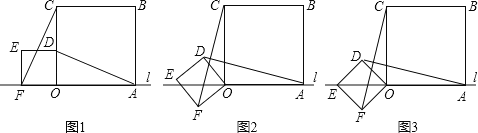
【题目】如图1，OA=2，OB=4，以A点为顶点，AB为腰在第三象限作等腰直角△ABC.

（1）求C点的坐标.

（2）如图2，OA=2,P为y轴负半轴上的一个动点，若以P为直角顶点，PA为腰作等腰直角△APD，过D作DE⊥x轴于E点，求OP－DE的值.

（3）如图3，点F坐标为（－4，－4），点G（0，m）在y轴负半轴，点H（n，0）在x轴的正半轴，且FH⊥FG，求m+n的值.

Answer 1

【答案】答案见解析.

【解析】

（1）作CD⊥AD，易证∠ACD=∠OAB，即可求证△ACD≌△BAO，可得AD=OB，CD=OA即可解题；

（2）作DF⊥OP，易证∠APO=∠PDF，即可证明△AOP≌△PFD，可得AO=PF，DE=OF，即可解题；

（3）作FD⊥HD，FE⊥OG，易证∠EFG=∠DFH，即可证明△EFG≌△DFH，可得EG=DH，即-m-4=n+4，即可解题．

解：如图，

（1）过点C作CD⊥AD，

∵∠CAD+∠ACD=90°，∠CAD+∠OAB=90°，

∴∠ACD=∠OAB，

在△ACD和△BAO中，

∴△ACD≌△BAO，（AAS）

∴AD=OB，CD=OA，

∴点C坐标为（-6，-2）；

(2)作DF⊥OP，

∵∠APO+∠DPF=90°，∠PDF+∠DPF=90°，

∴∠APO=∠PDF，

在△AOP和△PFD中，

∴△AOP≌△PFD，（AAS）

∴AO=PF，DE=OF，

∴OP-DE=OP-OF=FP=AO=2；

(3)作FD⊥HD，FE⊥OG，则FE=FD=4，

∵∠EFG+∠OFE=90°，∠OFE+∠DFH=90°，

∴∠EFG=∠DFH，

在△EFG和△DFH中， ，

∴△EFG≌△DFH，（ASA）
∴EG=DH，即-m-4=n+4，
∴m+n=-8．