题目内容
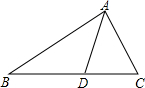如图所示，AD是△ABC的角平分线，且AB：AC=2：1，则△ABD与△ACD的面积比为 （ ）| A、2：1 | B、1：2 | C、4：1 | D、1：4 |
分析：过点D作DE⊥AB，DF⊥AC，垂足分别为E、F，根据角平分线上的点到角的两边的距离相等可得DE=DF，然后根据三角形的面积公式列式即可求出两三角形的面积的比值．
解答：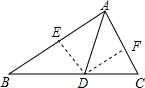
解：如图，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F，
∵AD是△ABC的角平分线，
∴DE=DF，
∴S△ABD=
AB•DE，S△ACD=
AC•DF，
∵AB：AC=2：1，
∴S△ABD：S△ACD=（
AB•DE）：（
AC•DF）=AB：AC=2：1．
故选A．
解：如图，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F，∵AD是△ABC的角平分线，
∴DE=DF，
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB：AC=2：1，
∴S△ABD：S△ACD=（
| 1 |
| 2 |
| 1 |
| 2 |
故选A．
点评：本题主要考查了角平分线上的点到角的两边的距离相等的性质，作出辅助线表示出三角形的面积是解题的关键．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
如图所示，AD是△ABC中BC边上的中线，已知△ABC的面积为12，则△ACD的面积等于
如图所示，AD是△ABC的中线，AB=6cm，AC=5cm，求△ABD和△ADC的周长的差．
55、如图所示，AD是∠BAC的平分线，DE⊥AB，垂足为E，DF⊥AC，垂足为F，且BD=CD．
26、已知如图所示，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，四边形AEDF是菱形吗？说明理由．
如图所示，AD是△ABC的高，AE是⊙O的直径，A，B，C三点都在圆上，∠DAC=30°，则∠BAE为（ ）