题目内容
在直角坐标系xOy中,设点A(0,t),点Q(t,b)(t,b均为非零常数),平移二次函数y=-tx2的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(|OB|<|OC|),连接AB。
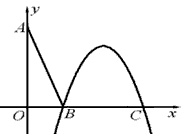
(1)是否存在这样的抛物线F,使得|OA|2=|OB|·|OC|?请你作出判断,并说明理由;
(2)如果AQ∥BC,且tan∠ABO=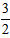 ,求抛物线F对应的二次函数的解析式。
,求抛物线F对应的二次函数的解析式。
(2)如果AQ∥BC,且tan∠ABO=
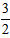 ,求抛物线F对应的二次函数的解析式。
,求抛物线F对应的二次函数的解析式。解:(1)∵平移y=-tx2的图象得到的抛物线F的顶点为Q,
∴抛物线F对应的解析式为:y=-t(x-t)2+b,
∵抛物线与x轴有两个交点,∴tb>0,令y=0,得OB=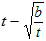 ,OC=
,OC=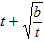 ,
,
∴|OB|·|OC|=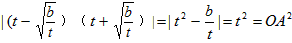 ,即
,即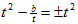 ,
,
所以当b=2t3时,存在抛物线F使得|OA|2=|OB|·|OC|;
(2)∵AQ∥BC,
∴t=b,得F:y=-t(x-t)2+t,
解得x1=t-1,x2=t+1,
在Rt△AOB中,①当t>0时,由|OB|<|OC|,得B(t-1,0),
当t-1>0时,由tan∠ABO=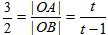 ,解得t=3,
,解得t=3,
此时,二次函数解析式为y=-3x2+18x-24;
当t-1<0时,由tan∠ABO=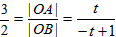 ,解得t=
,解得t=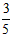 ,
,
此时,二次函数解析式为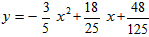 ;
;
②当t<0时,由|OB|<|OC|,将-t代t,可得t=-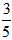 ,t=-3,
,t=-3,
所以二次函数的解析式为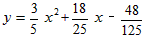 或
或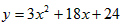 。
。
∴抛物线F对应的解析式为:y=-t(x-t)2+b,
∵抛物线与x轴有两个交点,∴tb>0,令y=0,得OB=
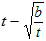 ,OC=
,OC=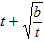 ,
,∴|OB|·|OC|=
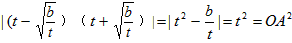 ,即
,即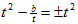 ,
,所以当b=2t3时,存在抛物线F使得|OA|2=|OB|·|OC|;
(2)∵AQ∥BC,
∴t=b,得F:y=-t(x-t)2+t,
解得x1=t-1,x2=t+1,
在Rt△AOB中,①当t>0时,由|OB|<|OC|,得B(t-1,0),
当t-1>0时,由tan∠ABO=
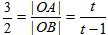 ,解得t=3,
,解得t=3,此时,二次函数解析式为y=-3x2+18x-24;
当t-1<0时,由tan∠ABO=
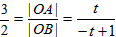 ,解得t=
,解得t=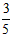 ,
,此时,二次函数解析式为
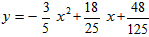 ;
;②当t<0时,由|OB|<|OC|,将-t代t,可得t=-
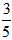 ,t=-3,
,t=-3,所以二次函数的解析式为
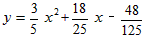 或
或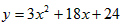 。
。
练习册系列答案
相关题目

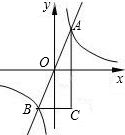 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.