Question

【题目】（1）已知a为正整数，关于x的不等式组的整数解仅2、3、4，则a的最大值是_____．

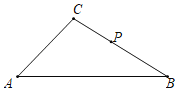
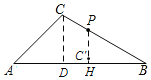
（2）如图，△ABC中，AC＝，∠A＝45°，∠B＝30°，P是BC边上一点（不含端点），将PC绕着点P逆时针旋转得到PC′，旋转角α（0＜α＜180°），若旋转过程中，点C′始终落在△ABC内部（不包含边上），则PC的取值范围是_____．

Answer 1

【答案】﹣20 0＜PC＜4

【解析】

（1）首先解不等式组，用a表示出不等式组的解集，根据不等式的整数解仅有2，3，4，即可确定a的值，从而求解；

（2）过C作CD⊥AB于D，过P作PH⊥AB于H，设CP＝x＝PC'，则BP＝12﹣x，PH＝（12﹣x），依据旋转过程中，点C′始终落在△ABC内部（不包括边上），即可得到PC'＜PH，即x＜（12﹣x），进而得出PC的取值范围．

（1）解不等式组得：﹣＜x≤，

∵整数解仅有2，3，4，

∴1≤﹣＜2，解得：﹣40＜a≤﹣20，

∴a的最大值为﹣20，

故答案为：﹣20；

（2）如图，过C作CD⊥AB于D，过P作PH⊥AB于H，

∵AC＝6，∠A＝45°，∠B＝30°，

∴AD＝CD＝6，BC＝2CD＝12，

设CP＝x＝PC'，则BP＝12﹣x，PH＝（12﹣x），

∵旋转过程中，点C′始终落在△ABC内部（不包括边上），

∴PC'＜PH，即x＜（12﹣x），

解得x＜4，

又∵PC＞0，

∴0＜PC＜4，

故答案为：0＜PC＜4．