题目内容
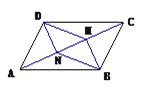
【题目】如图,AC是□ABCD的一条对角线,BM⊥AC, DN⊥AC,垂足分别为M,N,四边形BMDN是平行四边形吗?请选择一种你认为比较好的方法证明.
【答案】答案见解析
【解析】试题分析:由四边形ABCD是平行四边形,可得AD=BC,AD∥BC,又由BM⊥AC,DN⊥AC,即可得BM∥DN,∠DNA=∠BMC=90°,然后利用AAS证得△ADN≌△CBM,即可得DN=BM,由有一组对边相等且平行的四边形是平行四边形,即可证得四边形BMDN是平行四边形.
试题解析:解:四边形BMDN是平行四边形.理由如下:
∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠DAN=∠BCM.∵BM⊥AC,DN⊥AC,∴BM∥DN,∠DNA=∠BMC=90°,∴△ADN≌△CBM(AAS),∴DN=BM,∴四边形BMDN是平行四边形.

练习册系列答案
相关题目