Question

【题目】如图，在由边长为1的小正方形组成的网格图中有△ABC，建立平面直角坐标系后，点O的坐标是（0，0）．

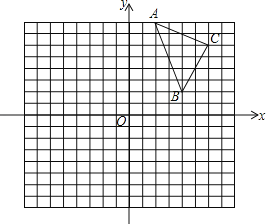
（1）以O为位似中心，作△A′B′C′∽△ABC，相似比为1：2，且保证△A′B′C′在第三象限；

（2）点B′的坐标为（ ， ）；

（3）若线段BC上有一点D，它的坐标为（a，b），那么它的对应点D′的坐标为（ ）．

Answer 1

【答案】（1）见解析；（2）﹣2，﹣1．（3）﹣，﹣．

【解析】

试题分析：（1）利用位似图形的性质进而得出△A′B′C′各顶点的位置，进而得出答案；

（2）利用所画图形，得出点B′的坐标；

（3）利用位似图形的性质得出点的坐标变化规律即可．

解：（1）如图所示：△A′B′C′即为所求；

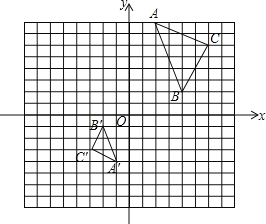
（2）点B′的坐标为：（﹣2，﹣1）；

故答案为：﹣2，﹣1．

（3）若线段BC上有一点D，它的坐标为（a，b），那么它的对应点D′的坐标为：（﹣，﹣）．

故答案为：﹣，﹣．