题目内容
【题目】如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.

(1)当∠BAM= °时,AB=2BM;
(2)请添加一个条件: ,使得△ABC为等边三角形;
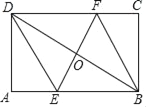
①如图1,当△ABC为等边三角形时,求证:CN+CM=AC;
②如图2,当点M运动到线段BC之外(即点M在线段BC的延长线上时),其它条件不变(△ABC仍为等边三角形),请写出此时线段CN、CM、AC满足的数量关系,并证明.
【答案】(1)30;(2)AB=AC;①证明见解析;②CN-CM=AC,理由见解析
【解析】
(1)根据含30°角的直角三角形的性质解答即可;
(2)利用含一个60°角的等腰三角形是等边三角形的判定解答;①利用等边三角形的性质和全等三角形的判定证明△BAM≌△CAN,从而利用全等三角形的性质求解;②利用等边三角形的性质和全等三角形的判定证明△BAM≌△CAN,从而利用全等三角形的性质求解.
解:(1)当∠BAM=30°时,
∴∠AMB=180°﹣60°﹣30°=90°,
∴AB=2BM;
故答案为:30;
(2)∵在△ABC中,∠B=60°
∴当AB=AC时,可得可得△ABC为等边三角形;
故答案为:AB=AC;
①如图1中,
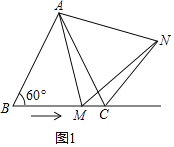
∵△ABC与△AMN是等边三角形,
∴AB=AC=BC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC﹣∠MAC=∠MAN﹣∠MAC,
即∠BAM=∠CAN,
在△BAM与△CAN中,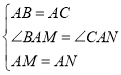 ,
,
∴△BAM≌△CAN(SAS),
∴BM=CN;
∴AC=BC=BM+CM=CM+CN
即CN+CM=AC;
②CN-CM=AC,
理由:如图2中,
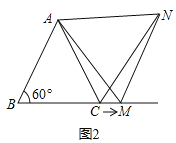
∵△ABC与△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC+∠MAC=∠MAN+∠MAC,
即∠BAM=∠CAN,
在△BAM与△CAN中,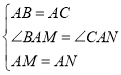 ,
,
∴△BAM≌△CAN(SAS),
∴BM=CN
∴AC=BC=BM-CM=CN-CM
即CN-CM=AC

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案