题目内容
【题目】“推进全科阅读,培育时代新人”.某学校为了更好地开展学生读书活动,随机调查了八年级50名学生最近一周的读书时间,统计数据如下表:
时间(小时) | 6 | 7 | 8 | 9 | 10 |
人数 | 5 | 8 | 12 | 15 | 10 |
(1)写出这50名学生读书时间的众数、中位数、平均数;
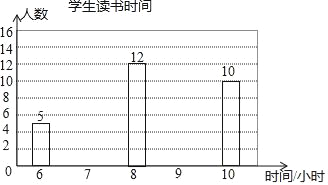
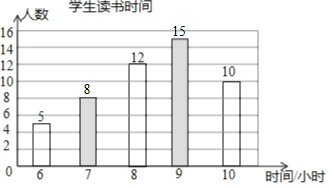
(2)根据上述表格补全下面的条形统计图.
(3)学校欲从这50名学生中,随机抽取1名学生参加上级部门组织的读书活动,其中被抽到学生的读书时间不少于9小时的概率是多少?
【答案】(1)众数是9;中位数是8.5;平均数是8.34;(2)补图见解析;(3)![]()
【解析】(1)先根据表格提示的数据得出50名学生读书的时间,然后除以50即可求出平均数;在这组样本数据中,9出现的次数最多,所以求出了众数;将这组样本数据按从小到大的顺序排列,其中处于中间的两个数是8和9,从而求出中位数是8.5;
(2)根据题意直接补全图形即可.
(3)从表格中得知在50名学生中,读书时间不少于9小时的有25人再除以50即可得出结论.
(1)观察表格,可知这组样本数据的平均数为:
(6×5+7×8+8×12+9×15+10×10)÷50=8.34,
故这组样本数据的平均数为8.34;
∵这组样本数据中,9出现了15次,出现的次数最多,
∴这组数据的众数是9;
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数是8和9,
∴这组数据的中位数为![]() (8+9)=8.5;
(8+9)=8.5;
(2)补全图形如图所示,
(3)∵读书时间是9小时的有15人,读书时间是10小时的有10人,
∴读书时间不少于9小时的有15+10=25人,
∴被抽到学生的读书时间不少于9小时的概率是![]()

练习册系列答案
相关题目