题目内容
【题目】如图,抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(3,0),于y轴交于C.
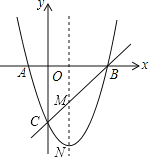
(1)求该抛物线的解析式;
(2)若M是抛物线的对称轴与直线BC的交点,N是抛物线的顶点,求MN的长;
(3)若点P是抛物线上点,当S△PAB=8时,求点P的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)MN=1;(3)(![]() ,4),(
,4),(![]() ,4),(1,﹣4).
,4),(1,﹣4).
【解析】
(1)把点A、B的坐标分别代入函数解析式,列出关于系数b、c的方程组,通过解方程组求得它们的值即
2)结合抛物线的解析式得到点C、N的坐标,利用B、C的坐标可以求得直线BC的解析式,由一次函数图象上点的坐标特征和点的坐标与图形的性质进行解答即可;
(3)根据P点在抛物线上设出P点,然后再由S△PAB=8,从而求出P点坐标
解:(1)如图1,∵抛物线y=x2+bx+c与x轴的两个交点分别为A(﹣1,0),B(3,0),
∴![]() ,
,
解得![]() ,
,
∴所求抛物线的解析式为:y=x2﹣2x﹣3;
(2)由(1)知,该抛物线的解析式为:y=x2﹣2x﹣3,则C(0,﹣3).
又∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴N(1,﹣4).
设直线BC的解析式为y=kx﹣3(k≠0).
把B(3,0)代入,得
0=3k﹣3,
解得k=1,则该直线解析式为:y=x﹣3.
故当x=1时,y=﹣2,即M(1,﹣2),
∴MN=|﹣3|﹣|﹣2|=1.即MN=1;
(3)设点P的坐标为(x,y),由题意,得
S△PAB=![]() ×4×|y|=8,
×4×|y|=8,
∴|y|=4,
∴y=±4.
当y=4时,x2﹣2x﹣3=4,
∴x1=1+2![]() ,x2=1﹣2
,x2=1﹣2![]() ,
,
当y=﹣4时,x2﹣2x﹣3=﹣4,
∴x=1,
∴当P点的坐标分别为(1+2![]() ,4)、(1﹣2
,4)、(1﹣2![]() ,4)、(1,﹣4)时,S△PAB=8.
,4)、(1,﹣4)时,S△PAB=8.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目