题目内容
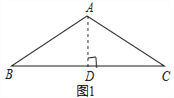
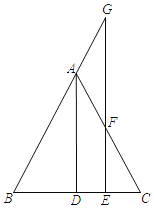
【题目】如图所示,△ABC中,AB=AC,AD平分∠BAC,点G是BA延长线上一点,点F是AC上一点,AG=AF,连接GF并延长交BC于E.
(1)若AB=8,BC=6,求AD的长;
(2)求证:GE⊥BC.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据题意可知AD⊥BC,BD=CD=3,再根据勾股定理即可解答
(2)根据题意可知GA=GF,得到∠G=∠AFG,再通过∠BAC=∠G+∠AFG=2∠AFG,∠BAC=2∠CAD,得到AD∥EG,即可解答
(1)∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD=3,
在Rt△ABD中,AD=![]() .
.
(2)∵GA=GF,
∴∠G=∠AFG,
∵∠BAC=∠G+∠AFG=2∠AFG,∠BAC=2∠CAD,
∴∠AFG=∠CAD,
∴AD∥EG,
∵AD⊥BC,
∴GE⊥BC.

练习册系列答案
相关题目