ΧβΡΩΡΎ»ί
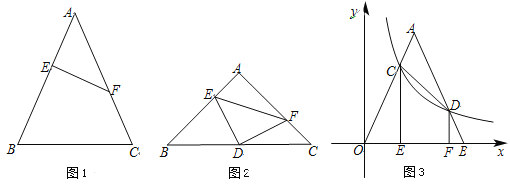
ΓΨΧβΡΩΓΩΕ®“εΘΚ»γΆΦ1Θ§Β»―ϋΓςABC÷–Θ§ΒψEΘ§FΖ÷±π‘Ύ―ϋABΘ§AC…œΘ§Ν§ΫαEFΘ§»τAEΘΫCFΘ§‘ρ≥ΤEFΈΣΗΟΒ»―ϋ»ΐΫ«–ΈΒΡΡφΒ»œΏΘ°
Θ®1Θ©»γΆΦ1Θ§EF «Β»―ϋΓςABCΒΡΡφΒ»œΏΘ§»τEFΓΆABΘ§ABΘΫACΘΫ5Θ§AE ΘΫ2Θ§«σΡφΒ»œΏEFΒΡ≥ΛΘΜ
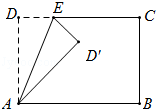
Θ®2Θ©»γΆΦ2Θ§»τΒ»―ϋ÷±Ϋ«ΓςDEFΒΡ÷±Ϋ«ΕΞΒψD«ΓΚΟΈΣΒ»―ϋ÷±Ϋ«ΓςABCΒΉ±ΏBC…œΒΡ÷–ΒψΘ§«“ΒψEΘ§FΖ÷±π‘ΎABΘ§AC…œΘ§«σ÷ΛΘΚEFΈΣΒ»―ϋΓςABCΒΡΡφΒ»œΏΘΜ
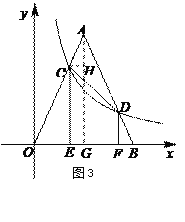
Θ®3Θ©»γΆΦ3Θ§Β»―ϋΓςAOBΒΡΕΞΒψO”κ‘≠Βψ÷ΊΚœΘ§ΒΉ±ΏOB‘Ύx÷α…œΘ§Ζ¥±»άΐΚ· ΐyΘΫ ![]() Θ®xΘΨ0Θ©ΒΡΆΦœσΫΜΓςOAB”ΎΒψCΘ§DΘ§»τCD«ΓΈΣΓςAOBΒΡΡφΒ»œΏΘ§ΙΐΒψCΘ§DΖ÷±πΉςCEΓΆx÷αΘ§DFΓΆx÷αΘ§“―÷ΣOEΘΫ2Θ§«σOFΒΡ≥ΛΘ°
Θ®xΘΨ0Θ©ΒΡΆΦœσΫΜΓςOAB”ΎΒψCΘ§DΘ§»τCD«ΓΈΣΓςAOBΒΡΡφΒ»œΏΘ§ΙΐΒψCΘ§DΖ÷±πΉςCEΓΆx÷αΘ§DFΓΆx÷αΘ§“―÷ΣOEΘΫ2Θ§«σOFΒΡ≥ΛΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΡφΒ»œΏEFΒΡ≥ΛΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©EFΈΣΒ»―ϋΓςABCΒΡΡφΒ»œΏΘΜ
Θ®3Θ©OFΘΫ2![]() ΘΪ2
ΘΪ2
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ(1)ΓΔΗυΨίΡφΒ»œΏΒΡΕ®“εΒΟ≥ωCF=AE=2Θ§AF=3Θ§ΗυΨίΙ¥Ι…Ε®άμΒΟ≥ωEFΒΡ≥ΛΕ»ΘΜ(2)ΓΔΝ§Ϋ”ADΘ§ΗυΨίΧβ“β÷ΛΟς≥ωΓςEDAΚΆΓςFDC»ΪΒ»Θ§¥”ΕχΒΟ≥ωAE=CFΘ§ΒΟΒΫΡφΒ»œΏΘΜ(3)ΓΔ…ηOF=xΘ§ΉςAGΓΆOBΘ§CHΓΆAGΘ§ΗυΨίΡφΒ»œΏΒΡ–‘÷ ΒΟ≥ωΓςACHΚΆΓςDBF»ΪΒ»Θ§¥”ΕχΒΟ≥ωEG=x-4Θ§ΗυΨίΓςACHΚΆΓςCOEœύΥΤΒΟ≥ωxΒΡ÷ΒΘ§¥”ΕχΒΟ≥ωxΒΡ÷ΒΘ§Φ¥OFΒΡ≥ΛΕ».
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏEF «Β»―ϋΓςABCΒΡΡφΒ»œΏ
ΓύCF ΘΫAEΘΫ2Θ§”÷ABΘΫACΘΫ5 ΓύAFΘΫ3 ΓΏEFΓΆAB ΓύEFΘΫ![]() ΘΫ
ΘΫ![]()
Θ®2Θ©Ν§ΫαADΘ§‘ΎΒ»―ϋRtΓςABC÷–Θ§ΒψDΈΣΒΉ±Ώ…œ÷–Βψ ΓύADΘΫCD«“ΓœADCΘΫ90Γψ
”÷ΓΏDEΘΫDF«“ΓœEDFΘΫ90Γψ ΓύΓœEDAΘΫ90ΓψΘ≠ΓœADFΘΫΓœFDC
ΓύΓςEDAΓ’ΓςFDC ΓύAEΘΫCF ΓύEFΈΣΒ»―ϋΓςABCΒΡΡφΒ»œΏ
Θ®3Θ©»γΆΦ3Θ§…ηOFΘΫxΘ§‘ρDFΘΫ![]() ΉςAGΓΆOBΘ§CHΓΆAG
ΉςAGΓΆOBΘ§CHΓΆAG
ΓΏCDΈΣΓςAOBΒΡΡφΒ»œΏ ΓύACΘΫBDΘ§”÷ΓœACHΘΫΓœAOBΘΫΓœDBF
«“ΓœAHCΘΫΓœAGOΘΫΓœDFB ΓύΓςACHΓ’ΓςDBF ‘ρEGΘΫCHΘΫBFΘ§AHΘΫDF
”÷AOΘΫABΘ§«“AGΓΆOB ΓύOGΘΫBG ΓύGFΘΫBGΘ≠BFΘΫOGΘ≠EGΘΫOE
Υυ“‘EGΘΫxΘ≠2Θ≠2ΘΫxΘ≠4 ΓΏΓςACHΓΉΓςCOE Γύ![]() ΘΫ
ΘΫ![]() Φ¥
Φ¥![]() ΘΫ
ΘΫ![]()
Μ·ΦρΒΟx2Θ≠4xΘ≠4ΘΫ0 Υυ“‘xΘΫ2![]() ΘΪ2 Φ¥OFΘΫ2
ΘΪ2 Φ¥OFΘΫ2![]() ΘΪ2
ΘΪ2

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ