题目内容
如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
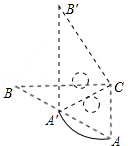

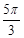
试题分析:根据Rt△ABC中的30°角所对的直角边是斜边的一半、直角三角形斜边上的中线等于斜边的一半以及旋转的性质推知△AA′C是等边三角形,所以根据等边三角形的性质利用弧长公式来求CA′旋转所构成的扇形的弧长:
∵在Rt△ABC中,∠B=30°,AB=10cm,∴AC=
 AB=5cm。
AB=5cm。根据旋转的性质知,A′C=AC,∴A′C=
 AB=5cm。
AB=5cm。∴点A′是斜边AB的中点,∴AA′=
 AB=5cm。
AB=5cm。∴AA′=A′C=AC,∴∠A′CA=60°。
∴CA′旋转所构成的扇形的弧长为:
 (cm)。
(cm)。
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 与半圆交于
与半圆交于 、
、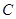 两点,且
两点,且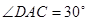 .
.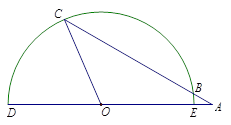
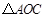 的面积
的面积


