题目内容
【题目】拼图是一种研究代数恒等式的重要方法,所谓的拼图指的是把所给的图形以不同的方式拼成不同形状的图形,把图形面积用不同的代数式表示,由于拼图前后的面积相等,从而相应的代数式的值也相等,进而得到代数恒等式.
(1)智慧学习小组探索了用4个如图1所示的全等的长方形(长、宽分别为a、b)拼成不同的图形.在研究过程中,他们用这4个长方形拼成了一个如图2所示的“回形”正方形.拼图前后,请写出该小组所用图形(4个长方形)的面积的计算方法:拼图前: ;拼图后: ;因为拼图前后的面积不变,所以可得代数恒等式: .

(2)利用(1)中得到的恒等式,解决下面的问题:已知![]() 求xy的值.
求xy的值.
(3)超人学习小组受智慧学习小组的启发,用4个如图3所示的全等的直角三角形(三边长分别为a、b、c)拼成了两种“中空”的正方形.请你画出这两种图形:
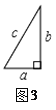
由上面的图形可得代数恒等式: .
(4)利用(3)中得到的代数恒等式,解决下面的问题:在Rt△ABC中,已知∠ABC=90°,AB=6,BC=8,求AC的长.
【答案】(1)4ab,(a+b)2 - (a-b)2,4ab = (a+b)2 - (a-b)2 ;
(2)![]() ;
;
(3)画图见解析,![]()
(4)AC= 10
【解析】(1)通过观察可以得大正方形边长为a+b,小正方形边长为a-b,利用大正方形面积减去小正方形面积即为阴影部分的面积,得出答案;(2)由(1)的结论变形后即可得出xy的值;(3)通过两个组合正方形的面积之间相等的关系即可证明勾股定理;(4)根据勾股定理:在如何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,即BC2=AC2+AB2,结合BC=10,AB=6,可求出另一条直角边AC的长度.
解:(1)拼图前:4ab
拼图后:(a+b)2 - (a-b)2
观察图形得:
大正方形边长为:a+b,
小正方形边长为:a-b,
根据大正方形面积-小正方形面积=阴影部分面积得:
4ab=(a+b)2-(a-b)2.
可得代数恒等式: 4ab = (a+b)2 - (a-b)2
故答案为:4ab = (a+b)2 - (a-b)2.
“点睛”本题考查了完全平方公式的几何背景,学生需要掌握完全平方公式和几何图形的关系即可,题目整体涉及很好,可以考查学生的观察能力.
(2)由(1)可得,4ab = (a+b)2 - (a-b)2,
∴ 4xy = (x+y)2 - (x-y)2
∴ ![]()
又∵ ![]() ,
,![]()
∴ ![]() ,
,![]()
∴![]() .
.
(3)如图所示,
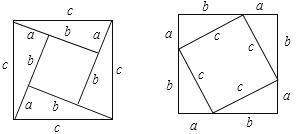
![]()
解:选用(1).
证明:∵S大正方形=c2
S大正方形=4S△+S小正方形=4×![]() ab+(b-a)2,
ab+(b-a)2,
∴c2=4×![]() ab+(b-a)2-c2=a2+b2;
ab+(b-a)2-c2=a2+b2;
选用(2):
证明:图中把大正方形的面积分了四分部,分别是:边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形.
∵根据面积相等得:(a+b)2=c2+b2+4×![]() ab,
ab,
由右图可得(a+b)2=c2+4×![]() ab,
ab,
∴a2+b2+4×![]() ab=c2+4×
ab=c2+4×![]() ab,
ab,
∴a2+b2=c2.
(4)∵在Rt△ABC中,∠ABC=90°,
∴ ![]() ,
,
又∵ AB=6,BC=8,
∴ ![]() .
.
∴ AC= 10.
“点睛”本题考查利用图形面积的关系证明勾股定理,解题关键是利用三角形和正方形边长关系进行组合图形.像这类直接考查定义的题目,解答的关键是熟练掌握勾股定理的定义及其在直角三角形中的表示形式.