题目内容
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在弧AB的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
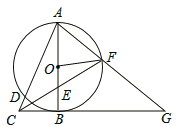
(1)求证:OF=![]() BG;
BG;
(2)若AB=4,求DC的长.
【答案】(1)证明过程见解析;(2)DC=![]()
【解析】
试题分析:(1)直接利用圆周角定理结合平行线的判定方法得出FO是△ABG的中位线,即可得出答案;(2)首选得出△FOE≌△CBE(ASA),则BC=FO=![]() AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
试题解析:(1)∵以Rt△ABC的直角边AB为直径作⊙O,点F恰好落在![]() 的中点,∴
的中点,∴![]() =
=![]() ,
,
∴∠AOF=∠BOF, ∵∠ABC=∠ABG=90°, ∴∠AOF=∠ABG, ∴FO∥BG, ∵AO=BO,
∴FO是△ABG的中位线, ∴FO=![]() BG;
BG;
(2)在△FOE和△CBE中,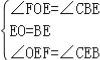 , ∴△FOE≌△CBE(ASA), ∴BC=FO=
, ∴△FOE≌△CBE(ASA), ∴BC=FO=![]() AB=2,
AB=2,
∴AC=![]() =2
=2![]() , 连接DB, ∵AB为⊙O直径, ∴∠ADB=90°, ∴∠ADB=∠ABC,
, 连接DB, ∵AB为⊙O直径, ∴∠ADB=90°, ∴∠ADB=∠ABC,
∵∠BCD=∠ACB, ∴△BCD∽△ACB, ∴![]() =
=![]() , ∴
, ∴![]() =
=![]() , 解得:DC=
, 解得:DC=![]() .
.


练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目