题目内容
【题目】如图,在平行四边形ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
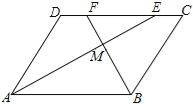
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
【答案】(1)证明见解析;(2)DF=CE,理由见解析.
【解析】试题分析:(1)利用平行四边形的性质得到AD∥BC,然后得到∠DAB+∠ABC=180°,然后根据角的平分线得出∠DAB=2∠BAE,∠ABC=2∠ABF,等量代换得出∠BAE+∠ABF=90°即可;(2)先猜想DF=CE,利用角的平分线和平行线的性质可得DE=AD,CF=BC,然后利用线段的和差关系可得出结论.
试题解析:(1)∵在平行四边形ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE、BF分别平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF.
∴2∠BAE+2∠ABF=180°.
即∠BAE+∠ABF=90°.
∴∠AMB=90°.
∴AE⊥BF.
(2)DF=CE,
∵在平行四边形ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又∵AE平分∠DAB,
∴∠DAE=∠EAB.∴∠DEA=∠DAE.
∴DE=AD.
同理可得,CF=BC.
又∵在平行四边形ABCD中,AD=BC,
∴DE=CF.
∴DE﹣EF=CF﹣EF.
即DF=CE.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目