Question

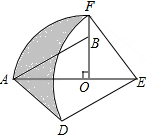
【题目】如图,正方形MNPQ网格中,每个小方格的边长都相等,正方形ABCD的顶点在正方形MNPQ的小方格顶点上.

(1)设正方形MNPQ网格内的每个小方格的边长为1,求:

①△ABQ,△BCM,△CDN,△ADP的面积;

②正方形ABCD的面积;

(2)设MB=a,BQ=b,利用这个图形中的直角三角形和正方形的面积关系,你能验证勾股定理吗?相信你能给出简明的推理过程.

Answer 1

【答案】(1)①6；②25；(2)见解析

【解析】试题分析：（1）根据直角三角形的面积公式：S=两条直角边的乘积的一半进行计算；

（2）根据面积能够验证勾股定理．

试题解析：解：（1）∵网格中每个小正方形的边长为1，由图可知AQ=3，BQ=4，∠Q=90°，∴S△ABQ=AQBQ=6；同理S△BCM=S△CDN=S△ADP=6．

又∵MQ=7，∴S正方形MNPQ=49，∴S正方形ABCD=S正方形MNPQ﹣4S△ABQ=49﹣4×6=25．

（2）能够验证勾股定理．理由如下：

在△BCM、△ABQ中，∵∠M=∠Q=∠ABC=90°，∴∠MBC=∠QAB．

又∵AB=BC，∴△BCM≌△ABQ．

同理△CDN≌△DAP≌△BCM．

∵MB=a，BQ=b，S正方形ABCD=S正方形MNPQ﹣4S△ABQ，∴AB2=（a+b）2﹣4×ab，即AB2=a2+b2．

设AB=c，得c2=a2+b2．